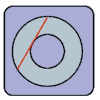
Remember
this problem? The one where you had to find the area between two circles by only knowing the length of the tangent "chord" (the red line)?
That problem is solved using some (moderately) tricky geometry. But if you know that the problem is solvable, it's actually pretty easy to solve by simply using the formula for the area of the circle and a bit of logic.
Can you do it?
We drop a perpendicular from the centre to the point where the line is a tangent to the inner circle. Then we see that the perpendicular drawn is the radius of the smaller circle and the line joining the centre to the point where the tangent to the smaller circle meets the larger circle is nothing but the radius of the larger circle. Hence by using Pythagoras Theorem for the right angled triangle thus formed, we see that the difference between the squares of the radii of the larger circle to that of the smaller circle is equal to the square of half the length of the line (in red) drawn in the picture. Thus the required area will be equal to 25(pi), where 'pi' is the ratio of the circumference to the diameter and its value is (22/7). Thus the required area is : 78.5 (approximately) square inches.
 Remember this problem? The one where you had to find the area between two circles by only knowing the length of the tangent "chord" (the red line)?
Remember this problem? The one where you had to find the area between two circles by only knowing the length of the tangent "chord" (the red line)?



