Look at this shape:
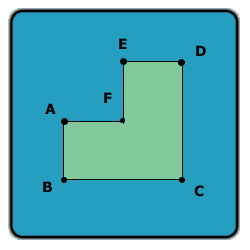
Assume AB = AF = FE = ED and BC = CD, and all the angles in the shape are 90 degrees.
Let A be the area of this shape (in cm^2), and P -- the perimeter of this shape (in cm).
If A - P is 60, what is the length of line AC?
(In reply to
answer by K Sengupta)
Let the sides BC =CD= y(say)
Then, A = y^2 -(y^2/4) = 3*(y^/4)
and, P = 2y+2y = 4y
Thus, by conditions of the problem:
3*(y^2/4) - 4y = 60
Or, 3*y^2 - 16y -240 = 0
Or, (y-12)(3y+ 20) = 0
Or, y = 12, ignoring the negative root which is inadmissible.
Consequently, AC = V(y^2 + (y^2)/4)
= V(6^2+12^2)
= 13.4164 units (approx.)
Edited on September 25, 2007, 1:38 pm



