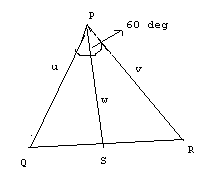
In triangle PQR, the respective length of the sides PQ and PR are denoted by u and v while the length of the median PS is denoted by w. It is known that w is the geometric mean of u and v, and Angle QPR = 60
o.
Determine |cos(Angle PQR) - cos(Angle QRP)|, where |x| denotes the
absolute value of x.
Hi!
Let note QR=s
1. Because w is median we can write from the median theorem
w^2=(2(u^2+v^2)-s^2))/4 = uv (because w^2=uv),
so i find that s=sqrt(2)|u-v| (1)
2.Cos theorem for u and v give us
u^2=v^2+s^2-2vscos(R)
v^2=u^2+s^2-2uscos(Q)
so i find
|cos(Q)-cos(R)| = ((v^2-u^2+s^2)/v-(u^2-v^2+s^2)/u)/(2s) (2)
3. Cos theorem for s give us
s^2=u^2+v^2-2uvcos(P) and because cos(P)=1/2
s^2=u^2+v^2-uv (3)
After replacing (3) in (2), i find
|cos(Q)-cos(R)| = 3|u-v|/(sqrt(2)*s) = 3/(2*sqrt(2)) = 1.0606
Edited on December 21, 2007, 5:10 pm
 In triangle PQR, the respective length of the sides PQ and PR are denoted by u and v while the length of the median PS is denoted by w. It is known that w is the geometric mean of u and v, and Angle QPR = 60o.
In triangle PQR, the respective length of the sides PQ and PR are denoted by u and v while the length of the median PS is denoted by w. It is known that w is the geometric mean of u and v, and Angle QPR = 60o. 


