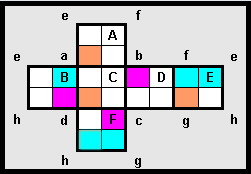
I applied one of the digits 1 through 9 to each cell of the provided net of a cube.
My object was to create a unique 4 digit square number on each face. At the same time I required each vertex to be a 3 digit square. I failed in that objective!
I have 6 unique 4 digit squares but I have duplicated just one of my vertices.
To emulate my "feat":
- a [Magenta]
Magenta cell is both the first digit of a 3 and 4 digit square
- an [Orange]
Orange cell signifies the first digit of only a 4 digit square, while
- a [Cyan]
Cyan cell signifies the first cell only of a 3 digit square.
The digits must be applied to each face by rotation, the direction is defined by need.
"A" through "F" represent the 6 faces of the cube while "a" through "h" represent the vertices of the cube when fully assembled.
 Note:
Note: Within the range allowed several squares utilise the same digits, and this is allowed by virtue of the commencement cell.
But then, there is still the challenge for 6 unique faces and 8 unique vertices.
(In reply to
re(2): Clarifications?? by ed bottemiller)
Apologies for the apparent lack of clarity.
Rotation of digits was meant to be clockwise or anticlockwise around the centre of a face (according to how you needed to construct the number). Similarly that applies around each vertex.
The coloured squares are the initial digit of each number with two colours being used as a sole starting location while the third colour initiates two numbers.
My Note? I had to think hard about myself as it was sometime ago when I wrote it. Reflect upon 12² and 21², 13² and 31², and 16² and 25²; each pair uses the same digits to compose their square but in a different order. For that reason I stipulated where numbers were to start. As such I could arrive at what I believe to be 6 unique 4 digit squares and 7 3digit squares, one of which is duplicated to form the twelfth.
My very last thought is to try to have 6 unique 4 digit square numbers and 8 unique 3 digit squares, naturally that may mean different initial stating positions which you would define.
Edited on April 30, 2008, 10:23 pm
|
|
Posted by brianjn
on 2008-04-30 20:44:52 |




