Trisecting an angle, using only compass and straight edge, was one of the great classical problems of antiquity.

Modern mathematics has proved it impossible, but here is a simple and ingenious mathematical cardboard device that trisects accurately:


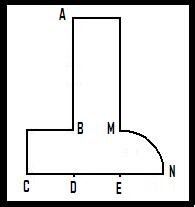
If you place it properly, so the edge AB passes through the vertex of the given angle, one side of the angle passes through point C, and the other side tangents the arc MN (arc of the circumference centered at E and radius ED), the lines traced from the vertex through the points D and E trisect exactly the angle.

Prove it.

The device is perfectly drawn to scale, so you can get any information you need about lengths, parallelism, intersections etc...

Call the vertex, located on line AB, V, and the point of tangency of the side that is tangent to arc MN, T.

As line AB, extended, is perpendicular to line CE, meeting that line at point D, triangle VCD is a right triangle, as is triangle VED.

Thus angles VDC and VDE are both right angles; segment VD equals itself by identity; and CD = DE, so the two right triangles are congruent and angle CVD = angle EVD.

Triangle VTE is also a right triangle with right angle at T.

TE = DE as the radius of arc MN, centered at E equals the length of segment DE. VE = VE by identity, so triangle VTE is congruent to triangle VDE, and angle TVE equals angle EVD.

These three equal angles, TVE, EVD and DVC, comprise the original angle TVC, and therefore trisect it.

Posted by Charlie on 2008-08-25 10:31:45