Each set of points {A,B,C}, {D,E,F} and {G,H,I} are equilaterally spaced and lie respectively upon the circumferences of 3 concentric circles centred at O.
The points D, A, B & I are collineal in that order as are F, C, A & H and E, B, C & G.
Scalene triangles GDB, HEC and IFA are formed by these points and contain Δ ABC in their overlapping.
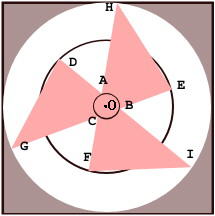
Note: This is not scaled.
Area "X" is that which is bounded by the scalene triangles (pink) while Area "Y" is all other areas (white) within the largest circle.
If line segment AB has a length of 1 unit and segment AI is 3 units:
1. What is the value of segment AF when the Pink region fills exactly half of the largest circle?
2. What is the proportion, Pink:White (or X:Y), when
/ AFI is a right angle? [I have considered X, the pink region, to equal 1 in my solution].
From ABC being equilateral and AB=1 we have OA=sqrt(3)/3
we also have that angle OAB=30.
Now we know OA=sqrt(3)/3 and AI=3 then we have
OI^2=AI^2+OA^2-2*AI*OA*cos(30)
OI^2=9+(1/3)-2*sqrt(3)*sqrt(3)/2
OI^2=9+(1/3)-3
OI^2=19/3
OI=sqrt(19)/sqrt(3)
OI=sqrt(57)/3
now for part 1.
if we let AF=x then we have the area of AFI as
3*x*sin(60)/2=3*x*sqrt(3)/4
and area of ABC is sqrt(3)/4
so the total area of the pink region is given by
(9x-2)*sqrt(3)/4
and we want this to be equal to half the area of the big circle which is 19pi/6
so we have
(9x-2)*sqrt(3)/4=19pi/6
27x*sqrt(3)-6*sqrt(3)=38*pi
27x-6=38pi*sqrt(3)/3
27x=(38pi*sqrt(3)+18)/3
x=(38pi*sqrt(3)+18)/81
or approximately 2.775
now for part 2.
Since the radius of the big circle is completely determined by the givens of AB=1 and AI=3 and we are also given that the pink area is 1, then the ratio must then be 3/(19pi) or approximately 0.0503
Edited on May 29, 2009, 4:10 am
|
|
Posted by Daniel
on 2009-05-28 16:19:04 |




