I tried approaching the problem from a geometrical point of view, instead of a trigonometrical one. I started with the principles that the interior angles of a triangle equal a straight angle (180°), and the base angle of an isosceles triangle are equal.
There was no division by any terms with variables, but still, the only answer I found was 60°, which is the degenerate case.
I now suspect that despite appearances, the arrangement is impossible, and that is what we need to show. I could probably even prove it to be impossible using calculus if I tried.
But Vohanam's comments still suggest that there is an AHA! approach I'm missing, so I'll keep working on it.
|
|
Posted by TomM
on 2002-06-18 16:51:28 |
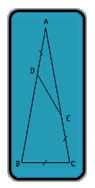 Given that:
Given that:


