|
Six days.
To prove the baron's statement can't be true for seven days, let's put a point corresponding to each day under consideration on a line and connect with an arrow the days for which we know GŁnnstefen shot fewer ducks (the beginning of the arrow) than on the second day (the end of the arrow). We get the following diagram:
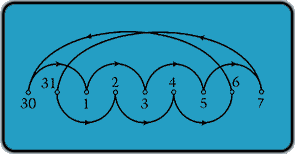
The chain of arrows is closed. Since each arrow represents an inequality, that means that the assumption that GŁnnstefen could make that statement for seven days was wrong
(you can't have a < b < c < a ).
If we consider only six days, it's easy to construct an example satisfying the conditions of the problem.
The statement is true for six days, August 1 through August 6.
Let xn represent the number of ducks shot on day n, with day 1 being July 30:
... 28 29 30 31 1 2 3 4 5 6 7 ...
... x1 x2 x3 x4 x5 x6 x7 x8 x9 ...
Then, from the statements we are taking to be true, we know that:
x1 > x3 > x5 > x7
and
x2 > x4 > x6 > x8
Also, from the statement made on the sixth, x1 > x8.
That yields the complete series of inequalities:
x2 > x4 > x6 > x8 > x1 > x3 > x5 > x7.
If we say that he shot 1 duck on July 31 (x2), and replace each " > " with " + 1 = ", we get the set of values:
... 28 29 30 31 1 2 3 4 5 6 7 ...
... 5 1 6 2 7 3 8 4 ...
Then, just say he shot more than 9 ducks every day for the week before July 29th (so that the second part of each statement is true), and the solution is clearly valid.
Thus, the greatest number of consecutive days for which the Baron's statement could be true is six (we have shown that it is possible, and that it is impossible for the seventh day under any circumstance). |




