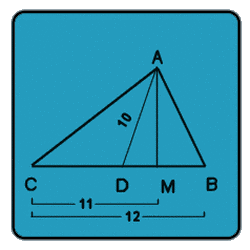
AC is 14.
Just takes two applications of the Pythagorean Theorem:
DC is 6 so DM is 5 and triangle MDA is a right triangle, so by the Pythagorean Theorem, MA is Square root of 75. But triangle MCA is also a right triangle, so by Pythagoras, AC^2 = 75 + 11^2. AC^2 = 196, so AC = 14.