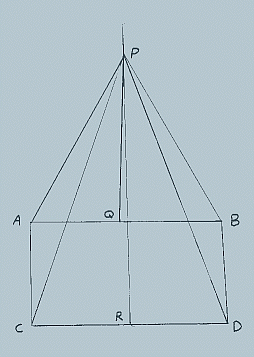
- In the figure, above AC=BD.
- ‹ACD is a right angle.
- ‹BDC is less than 90º.
- QP and RP are perpendicular bisectors of AB and CD respectively, intersecting at P.
- AP=BP and CP=DP because all points on the perpendicular bisector of a line are equidistant from the extremities of the line.
- Triangle APC is therefore congruent to triangle BPD because of the well known "side-side-side" theorem.
Now, ‹PCD=‹PDC because the base angles of an isosceles triangle are equal.
- ‹ACP=‹BDP because they are corresponding parts of congruent triangles.
- Of course, ‹ACP + ‹PCD = ‹BDP + ‹PDC because when equals are added to equals the results are equal.
Therefore, ‹ACD = ‹BDC.
But, wait, we know that this isn't true!
A mathematician had a rickety table (with top AB sitting on the floor CD with legs AC and BD) and had constructed the drawing above in an ineffectual effort to straighten the table. Can you figure out what is wrong?
Point P is so high up that, even with the slightness of the inward leaning of line DB, that is still enough that line PD passes to the right of point B. Thus angle BDC is not equal to angle BDP plus angle PDC, but rather, angle PDC
minus angle BDP.
The following spreadsheet results show how angle PBD, taken on the left side, is more than 180 degrees, as line QP is over 113 units long, under the assumption that AC=1, CD=2, DB=1 and angle CDB=89 degrees:
What Can You Prove?
Assuming AC=1, CD=2, DB=1 Angle CDB 89
Diagonal CB B3 2.220403201 (=SQRT(1+4-4*COS($E$2*PI()/180)))
Angle BCD B4 26.76293713 (=ASIN(SIN($E$2*PI()/180)/B3)*180/PI())
AB B5 1.982547599 (=SQRT(1+B3^2-2*B3*COS((90-B4)*PI()/180)))
Angle BAC B6 89.99559838 (=ASIN(B3*SIN((90-B4)*PI()/180)/B5)*180/PI())
A to line RP along AB B7 1.000000003 (=1/COS((90-B6)*PI()/180))
Q to intersection of RP with AB 0.008726203 (=B7-B5/2)
QP B9 113.5887264 (=B8*TAN(B6*PI()/180))
Angle BPQ B10 0.500000003 (=ATAN(B5/2/B9)*180/PI())
Angle PBQ B11 89.5 (=90-B10)
Angle ABD B12 91.00440162 (=360-$E$2-90-B6)
Angle PBD B13 180.5044016 (=B12+B11)
----
The formulas are shown to the right of the calculated cells. The 89 is in cell E2, and each calculated cell is in column B, starting at row 3 (I've marked most of them for reference). The law of cosines and law of sines have been used.
The internal angle being over 180 degrees indicates that in fact line PD is outside the main figure (to the right of B).
Edited on January 14, 2004, 9:17 am
|
|
Posted by Charlie
on 2004-01-14 09:15:28 |




