Begin with an arbitrary, convex quadrilateral. Next, draw squares outwardly on the sides of the quadrilateral, and join the centers of opposite squares.
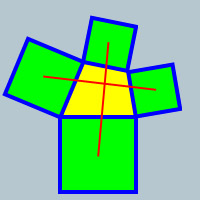
You might find the the two resulting lines are equal in length and intersect at precisely 90 degrees.
Prove (or disprove) the notion, that this is always true.
This is known as "Van Aubel's Theorem", and here is
a nice proof involving complex numbers.
Edited on January 10, 2004, 9:30 am



