 Remember this one?
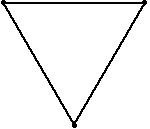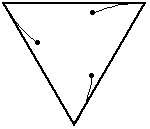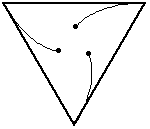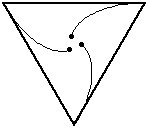
Remember this one?In this problem, the three bugs start at the corners of an equilateral triangle (with side length=10 inches).
Again, the bugs travel directly towards their neighbor (counter-clockwise). And, again, each bug homes in on its target, regardless of its target's motion. So, their paths will be curves spiraling toward the center of the triangle, where they will meet.
What distance will the bugs have covered by then, and how did you determine it?



