You may find this problem similar.

In a cube of side 4, I pack eight spheres of unit radius.

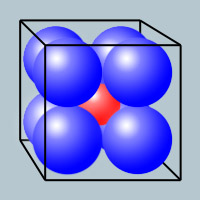
What is the largest sphere I can place in the center (such that it doesn't overlap any of the other spheres)?

Each large sphere touches the face of the cube at a distance of √2 from its closest corner.
Thus the centre of each sphere is √3 from its nearest corner.
Each diagonal is √(4^2 + 4^2 + 4^2) = √48
Therefore, the radius of the small sphere = (√48 - 2√3 - 2)/2 = √3 - 1


Edited on February 9, 2004, 7:27 am
Edited on February 9, 2004, 7:28 am

Posted by retiarius on 2004-02-09 07:26:20