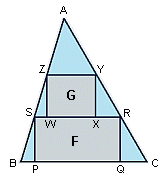
ABC is an acute-angled triangle with area 1. A rectangle F(PQRS) has its vertices on the sides of the triangle, with P and Q on BC, R on AC, and S on AB. Another rectangle, G(WXYZ), has its vertices on the sides of triangle ASR, with W and X on RS, Y on AS, and Z on AR.
What is the maximum total area of F and G?
(In reply to
Possible solution by Federico Kereki)
F.K., you wrote:
"Through S draw a parallel to BC; let T be its intersection with BC..."
But there is no intersection with BC if it is parallel. And the
same goes for your parallel through Z. Do you mean "drop a
perpendicular"?
-SK



