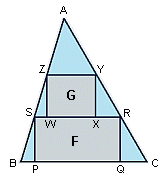
ABC is an acute-angled triangle with area 1. A rectangle F(PQRS) has its vertices on the sides of the triangle, with P and Q on BC, R on AC, and S on AB. Another rectangle, G(WXYZ), has its vertices on the sides of triangle ASR, with W and X on RS, Y on AS, and Z on AR.

What is the maximum total area of F and G?

So long as the base and the altitude are the same, the result will be the same regardless of whether the triangle is isosceles or not, so we'll make it isosceles.

The results will be proportional to the height and base of the triangle, so we can assume a standard triangle with altitude 1 and base 1, and scale up the results.

Call the length of an altitude of the triangle AZY x, and the altitude of triangle ASR y.

Rectangle F has height (1-x) and width equal to x.

Rectangle G has height (x-y) and width equal to y.

The total area of the two rectangles is then A = (1-x)x + (x-y)y, which is equal to

A = x - x² + yx - y²

∂A/∂x = 1 - 2x + y = 0

∂A/∂y = x - 2y = 0

so x=2y and 1 - 4y + y = 0, so y = 1/3.

The horizontal lines for the rectangles are 1/3 and 2/3 of the way down the triangle to maximize the area.

Then A = (1/3)(2/3) + (1/3)(1/3) = 1/3 for a triangle whose area is 1/2.

Scaling up, A = base * height / 3, or 2/3 the area of the triangle as a whole.

Posted by Charlie on 2004-03-02 15:36:59