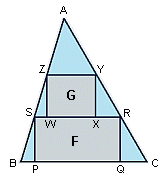
ABC is an acute-angled triangle with area 1. A rectangle F(PQRS) has its vertices on the sides of the triangle, with P and Q on BC, R on AC, and S on AB. Another rectangle, G(WXYZ), has its vertices on the sides of triangle ASR, with W and X on RS, Y on AS, and Z on AR.

What is the maximum total area of F and G?

(In reply to re(2): We are not square (in my original post, they are) by Juggler)

"for the particular figures that i used in the example, squares are required."

Why? If you assume that they need be squares, then you are not finding the maximum of anything, just calcluating an area. In fact, when you maximize the areas, the two rectangles will have the same height (one third of the height of the triangle), so both will never be squares (the bottom one is obviously much wider).

     /\
    /__\
   /|  |\
  / |  | \
 /|      |\
/ |      | \

Posted by DJ on 2004-03-03 13:39:12