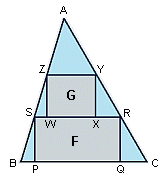
ABC is an acute-angled triangle with area 1. A rectangle F(PQRS) has its vertices on the sides of the triangle, with P and Q on BC, R on AC, and S on AB. Another rectangle, G(WXYZ), has its vertices on the sides of triangle ASR, with W and X on RS, Y on AS, and Z on AR.
What is the maximum total area of F and G?
The area of AYZ must equal the area of SWZ + RXY and the area of BPS + CQR. Because area is based on squares if any one of these areas gets larger it will get larger faster than the others get smaller. This means R and Y cut segment AC into thirds. Likewise S and Z cut segment AB into thirds. The area of AYZ is (1/3)² or 1/9. The total area within ABC but outside F and G is 3(1/9) or 1/3. Therefore the area of F+G=1-(1/3)=2/3.
|
|
Posted by Axorion
on 2004-03-03 19:27:47 |



