Remember
"Four Bugs" or
"Three Bugs"?
In this problem, the six bugs start at the corners of a regular hexagon (with side length=10 inches).
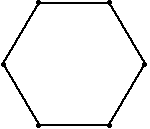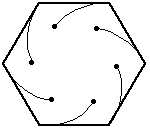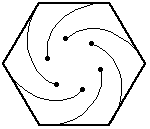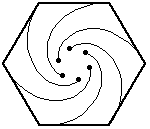
Again, the bugs travel directly towards their neighbor (counter-clockwise). And, again, each bug homes in on its target, regardless of its target's motion. So, their paths will be curves spiraling toward the center of the hexagon, where they will meet.
What distance will the bugs have covered by then, and how did you determine it?
(In reply to
Problem Solution With Explanation by K Sengupta)
generalised version of this problem would be as follows:
"There are N bugs and each of tese n bugs start at the corners of a regular N-gon (with side length=10 inches). The bugs travel directly towards their neighbor (counter-clockwise). And, again, each bug homes in on its target, regardless of its target's motion. So, their paths will be curves spiraling toward the center of the hexagon, where they will meet.
What distance will the bugs have covered by then, and how did you determine it?"
SOLUTION To The Generalised Version:
Let the regular N-gon be denoted by A_1A_2....A_n.
At any given instant, the three bugs located at each of the vertices A_1, A_2, ..., A_N of the n-gon which shrinks and rotates as the N bugs move closer together. Thus, the N bugs will describe N congruent logarithmic spirals that will meet at the center of the regular N-gon.
Since each angle of a regular n-gon is (180 - 360/N) degrees, it
follows that the path of the pursuer and the pursued will describe an angle of (180 - 360/N) degrees between them and consequently, each bug’s motion will have a component equal to cos (180 - 360/N) = - cos (360/N) times its velocity that will carry it towards its pursuer. Thus, these two bugs will have a mutual approach speed of 1 - cos(360/N) times the velocity of each bug.
Consequently, the distance traversed by each of the N bugs
until they meet at the center of the regular hexagon triangle
= 10/(1- cos(360/N)) inches
 Remember "Four Bugs" or "Three Bugs"?
Remember "Four Bugs" or "Three Bugs"?


