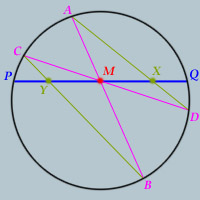
Given a circle and two points on that circle, P and Q, draw the chord PQ, and label its midpoint M.

Now draw two other chords of the circle AB and CD that both pass through M.

Further, draw chords AD and BC.

Label the intersection of AD and PQ, point X.
Label the intersection of BC and PQ, point Y.
_____________________________

Prove that M is the midpoint of line segment XY.

maybe it'll help some of you::

i'll use <A to represent angle A, etc.

<A = <C (share arc. BD)

<D = <B (share arc AC)

<CMY = <DMX (Vertical Angles)

<BMC = < DMA (vertical angles)

<AMX = <BMY (congruent - congruent implies congruent)

Tri. AMD ~ Tri. BMC (AA similarity)

In my opinion, to solve this problem we don't need all that reflection stuff, we just need to prove that <C = <D, and that M bisects CD. That seems simple enough, i just haven't been able to do it yet...

hope i helped

 

Posted by Derek on 2004-03-28 15:21:41