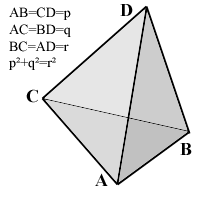
The pictured tetrahedron has four identical rectangular (i.e., right-angled or pythagorean) triangles as faces, with
AB=CD=p,
AC=BD=q,
AD=BC=r,
and p²+q²=r².
What's its volume, as a function of p, q and r?
D, if it exists, is the intersection of four different spheres:
* a sphere with radius r and certer at A
* a sphere with radios q and center at B
* a sphere with radius p and cneter at C
* a sphere with diameter r and center at the midpoint of BC
It's easy to see that if D is the symmetric of A with regard to the
midpoint of BC, then D satisfies all four coinditions, but it should be
proved that no otherp oint also does.
|
|
Posted by e.g.
on 2004-04-26 12:25:38 |
 The pictured tetrahedron has four identical rectangular (i.e., right-angled or pythagorean) triangles as faces, with
The pictured tetrahedron has four identical rectangular (i.e., right-angled or pythagorean) triangles as faces, with


