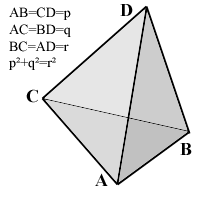
The pictured tetrahedron has four identical rectangular (i.e., right-angled or pythagorean) triangles as faces, with
AB=CD=p,
AC=BD=q,
AD=BC=r,
and p²+q²=r².
What's its volume, as a function of p, q and r?
(In reply to
Solution by Victor Zapana)
From http://www.mathpages.com/home/kmath226.htm:
In the preceding discussion we developed a tetrahedral version of
Heron's formula for a restricted class of tetrahedra, namely those
that can serve as the hypotenuse of a "right" 4D simplex, but there
are other special classes of tetrahedra that possess interesting
volume formulas. The one that gives the closest analogue to Heron's
formula is the class of tetrahedra whose opposite edges lengths
are equal. Thus there are only three independent edge lengths, and
each face of the tetrahedron is identical. Letting (a,f), (b,e), and
(c,d) denote the pairs of opposite edge lengths, we can set a=f, b=e,
and c=d in the basic determinant expression for the volume, or
equivalently in Piero della Francesca's formula, and we find that
the resulting expression for the squared volume factors as
72 V^2 = (-a^2 + b^2 + c^2)(a^2 - b^2 + c^2)(a^2 + b^2 - c^2)
which is certainly reminiscent of Heron's formula for the area of
each face
16 A^2 = (a+b+c)(-a+b+c)(a-b+c)(a+b-c)
This also shows that if each face is an identical right triangle, the
volume is zero, as it must be, since four such triangles connected
by their edges to give a tetrahedron necessarily all lie flat in the
same plane:
________
|\ /|
| \ / |
| \ / |
| \/ |
| /\ |
| / \ |
| / \ |
|/______\|
Obviously we can construct a regular tetrahedron with equilateral
triangles of the same area as these right triangles, and the volume
is V = a^3 / sqrt(72), which illustrates the fact that the face
areas of a tetrahedron do not in general determine it's volume.
|
|
Posted by Charlie
on 2004-04-26 20:55:42 |
 The pictured tetrahedron has four identical rectangular (i.e., right-angled or pythagorean) triangles as faces, with
The pictured tetrahedron has four identical rectangular (i.e., right-angled or pythagorean) triangles as faces, with


