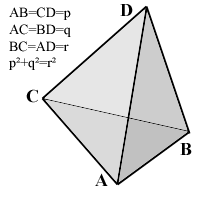
The pictured tetrahedron has four identical rectangular (i.e., right-angled or pythagorean) triangles as faces, with
AB=CD=p,
AC=BD=q,
AD=BC=r,
and pē+qē=rē.
What's its volume, as a function of p, q and r?
Yes yes, I know, everyone has already figured out the volume is zero. But I just wanted to share my thought processes in case it helped others. So this is pretty much my stream of consciousness from the beginning of trying to solve the problem:
Volume = 1/3*BaseArea*Height = 1/3*(p*q/2)*height. So the height is going to be the tough part.
Let's give the points coordinates:
A = (0, 0, 0), B = (p, 0, 0), C = (0, q, 0), D = (x, y, z)
(DA)^2 = r^2 = (x-0)^2 + (y-0)^2 + (z+0)^2 = x^2 + y^2 + z^2
(DB)^2 = q^2 = (x-p)^2 + (y-0)^2 + (z+0)^2 = x^2 2xp + p^2 + y^2 + z^2
(DC)^2 = p^2 = (x-0)^2 + (y-q)^2 + (z+0)^2 = x^2 + y^2 2yq + q^2 + z^2
Rearranging stuff around, we get:
x^2 + y^2 + z^2 = r^2 (1)
x^2 + y^2 + z^2 = q^2 p^2 + 2xp (2)
x^2 + y^2 + z^2 = p^2 q^2 + 2yq (3)
So (1) = (2) gives us:
(r^2 + p^2 q^2)/(2p) = x = [(p^2 + q^2) + p^2 q^2]/(2p) = (2p^2)/(2p) = p = x
And (1) = (3) gives us:
(r^2 + q^2 p^2)/(2q) = y = [(p^2 + q^2) + q^2 p^2]/(2q) = (2q^2)/(2q) = q = y
Substituting the newly found x and y values into (1) we get:
r^2 = x^2 + y^2 + z^2 = p^2 + q^2 + z^2 = p^2 + q^2
z^2 = 0 hmmmmmm, how can that be?
<lots of thinking, and trying to find a math mistake so I can find the height of the tetrahedron>
Hunh, look at that I fell for it =). The volume IS zero. Consider triangles A-B-D and A-C-D. Now draw a rectangle with sides p and q. Draw the diagonal of this rectangle, which is r. Hmm, this looks our two triangles laying flat next to each other, A-B-D-C around the rectangle. Since triangle A-B-C (or D-C-B) has a right angle at A (or D), then all we have to do is "fold" this rectangle on it's diagonal, and try to make a right angle between edge AB and edge AC (or edge BD and edge CD, same thing). But wait, the angle between AB and AC is already a right angle in the rectangle. Folding the rectangle will only make this angle smaller. So the only way to keep those right angles is to leave those two triangles in the rectangle (flat). A flat 3D object has a volume of zero.
Don't believe this "proof"? Ok, try this. Take two sheets of printer paper (or any two identical rectangles of paper) and lay them on top of each other, so all 4 corners on one piece lines up with all 4 corners on the other. Now fold the two pieces of paper together, along one of the diagonals and make a crease. Essentially, you've made 4 identical right triangles. Now separate the two pieces of paper, and line up the equal edges and try to make a tetrahedron that isn't flat. I don't think you'll be able to do it =)
Another way to think about it is that at any vertex of a tetrahedron, you have 3 angles (one on each face at that vertex). I don't have a proof for this, but it makes sense that the sum of any two angles must always be greater than the third angle. This is analogous to the rule for triangles, that the sum of any two sides must always be greater than the third side, except different dimensions. In a triangle, if the sum of any two of the 1D edges equals the third 1D edge, then the 2D area will be zero. And in a tetrahedron, if the sum of any two of the "2D" angles equals the third "2D" angle, then the 3D volume will be zero. I don't know how to prove this except to say draw any angle alpha <= 180. Create another ray, originating at the vertex of alpha, and dividing alpha into two smaller angles, beta and gamma. By the nature of how we created beta and gamma, beta + gamma = alpha. Represent these three angles with three pieces of paper, such that the edges of beta and gamma are not attached to each other, but are each attached to the edges of alpha. You will see that the only way you can get the edges of beta and gamma to touch is to lay those angles flat on alpha. If beta + gamma > alpha (AND beta + alpha > gamma AND alpha + gamma > beta), you would have some space between the three faces. If beta + gamma < alpha, then alpha's face would have to buckle and would no longer be a planar surface. This would be like if sides of triangle ABC had B+C<A. B and C could only reach each other if A bends, and would no longer be a straight edge.
Since we are dealing with identical right triangles, we know that one of the angles in each triangular face is 90, and the sum of the other two equals 90 (since the sum of all three has to be 180). So at a vertex, you have one of each of these angles of the triangle, so you do have two angles whose sum equals the third angle, resulting in a volume of zero!
Later!
Edited on April 28, 2004, 10:57 pm
|
|
Posted by nikki
on 2004-04-28 22:47:20 |
 The pictured tetrahedron has four identical rectangular (i.e., right-angled or pythagorean) triangles as faces, with
The pictured tetrahedron has four identical rectangular (i.e., right-angled or pythagorean) triangles as faces, with


