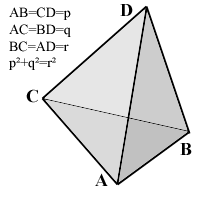
The pictured tetrahedron has four identical rectangular (i.e., right-angled or pythagorean) triangles as faces, with
AB=CD=p,
AC=BD=q,
AD=BC=r,
and p²+q²=r².
What's its volume, as a function of p, q and r?
Given p^2 + q^2 = r^2, the Pythagorean equation for a right triangle in Euclidean geometry, it can be seen that the shape is NOT a three-dimensional tetrahedron but a two-dimensional tetragon with parallel sides of lengths p and q (thus a paralleogram) with polygon diagonals of length r. Thus the shape has no volume but area only.
The AREA of the TETRAGON is then pq.
|
|
Posted by Dej Mar
on 2007-12-06 11:17:48 |
 The pictured tetrahedron has four identical rectangular (i.e., right-angled or pythagorean) triangles as faces, with
The pictured tetrahedron has four identical rectangular (i.e., right-angled or pythagorean) triangles as faces, with


