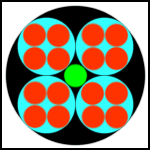
Begin with one
BLACK circle, and inscribe 4 identical, interior, cyclically tangent,
CYAN circles, such that they are also tangent to the black circle.
In each of the four cyan circles, inscribe 4 RED interior circles in exactly the same way.
Finally, inscribe a small GREEN circle in the center of the original black circle, tangent to the cyan circles.
Which is larger, this small green circle, or one of the small red circles?
If you rotate the black circle (and its contensts) 45°, then draw diagonals on the square, and draw lines connecting the midpoints of the sides of the square...
then you can see that the 4 centers of the cyan circles create another square.
1/2 the length of a side of this new square is obviously the radius of the cycan circle, but you can also see that this new square attaches to a quadrant of the original square at a distance r from the midpoints of the larger square.
Doing some calculation with the side of the original square being 2, the radius of the cycan circle is √(2) - 1 = 0.4142...
Just some thoughts...
|
|
Posted by Erik O.
on 2004-06-16 14:50:41 |
 Begin with one BLACK circle, and inscribe 4 identical, interior, cyclically tangent, CYAN circles, such that they are also tangent to the black circle.
Begin with one BLACK circle, and inscribe 4 identical, interior, cyclically tangent, CYAN circles, such that they are also tangent to the black circle.


