 How can you guarantee that you can cut an obtuse triangle into smaller triangles, all of which are acute? An obtuse triangle is a triangle with one obtuse angle. An acute triangle is a triangle with three acute angles. A right angle is neither acute nor obtuse.
If you can find such a dissection, what is the smallest number of acute triangles into which any obtuse triangle can be dissected?
How can you guarantee that you can cut an obtuse triangle into smaller triangles, all of which are acute? An obtuse triangle is a triangle with one obtuse angle. An acute triangle is a triangle with three acute angles. A right angle is neither acute nor obtuse.
If you can find such a dissection, what is the smallest number of acute triangles into which any obtuse triangle can be dissected?
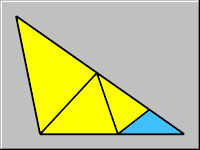
The graphic shows how this obtuse triangle can be divided into almost all acute triangles except one - the blue one. What approach should be used when one must cut an obtuse triangle into acute triangles only?
(In reply to
Answer in seven by Old Original Oskar!)
Another way to visualize the same construction:
First, why is the triangle obstuse? Because the other two angles are so darn small. So let's get rid of them.
Step 1. Lop off the two acute ends making 2 isosceles triangles. Now we have 2 acute triangles and one obtuse pentagon. All the angles in our pentagon have angles greater than 90.
Step 2. Pick a point in the center of the pentagon and from it draw a line to each vertex of the pentagon making 5 more acute triangles.
What about a proof?
IF step 1 is the way we begin, then it is obvious that 7 is the minimum. But maybe there is another 'winning' first step. My first cuts are from a side to a side. Any method that starts with cutting from a vertex to a side doesn't help since it makes a new obtuse or 2 right angles; vertex to vertex (in a triangle) is impossible, so any first step that cuts all the way across the triangle has to be from a side to a side.
Not sure it's a total proof, but it is close.
I haven't proved that all obtuse pentagons can be pentasected into 5 triangles where all the triangles are acute.
|
|
Posted by Larry
on 2004-08-07 08:22:07 |
 How can you guarantee that you can cut an obtuse triangle into smaller triangles, all of which are acute? An obtuse triangle is a triangle with one obtuse angle. An acute triangle is a triangle with three acute angles. A right angle is neither acute nor obtuse.
If you can find such a dissection, what is the smallest number of acute triangles into which any obtuse triangle can be dissected?
How can you guarantee that you can cut an obtuse triangle into smaller triangles, all of which are acute? An obtuse triangle is a triangle with one obtuse angle. An acute triangle is a triangle with three acute angles. A right angle is neither acute nor obtuse.
If you can find such a dissection, what is the smallest number of acute triangles into which any obtuse triangle can be dissected?



