 How can you guarantee that you can cut an obtuse triangle into smaller triangles, all of which are acute? An obtuse triangle is a triangle with one obtuse angle. An acute triangle is a triangle with three acute angles. A right angle is neither acute nor obtuse.
If you can find such a dissection, what is the smallest number of acute triangles into which any obtuse triangle can be dissected?
How can you guarantee that you can cut an obtuse triangle into smaller triangles, all of which are acute? An obtuse triangle is a triangle with one obtuse angle. An acute triangle is a triangle with three acute angles. A right angle is neither acute nor obtuse.
If you can find such a dissection, what is the smallest number of acute triangles into which any obtuse triangle can be dissected?
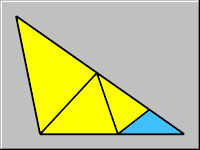
The graphic shows how this obtuse triangle can be divided into almost all acute triangles except one - the blue one. What approach should be used when one must cut an obtuse triangle into acute triangles only?
Well, some inovation from Larry's answer, I get 6 triangles, the minimum of course!
Same as Larry:
Lop off the two acute ends making 2 isosceles triangles. Now we have 2 acute triangles and one obtuse pentagon. All the angles in our pentagon have angles greater than 90.
But! Let the two constructed lines meet at one of the sides!
It is hard to explain, it will be better if I can provide a biagram, but I cannot.
Anyway, my answer is 6!
Vehe!
Anyway, I think mine of Larry's method will not work as the triangles constucted by Larry's pentagon, (mine is a quadrilateral), may result in one or some obtuse triangles! Sigh!
 How can you guarantee that you can cut an obtuse triangle into smaller triangles, all of which are acute? An obtuse triangle is a triangle with one obtuse angle. An acute triangle is a triangle with three acute angles. A right angle is neither acute nor obtuse.
If you can find such a dissection, what is the smallest number of acute triangles into which any obtuse triangle can be dissected?
How can you guarantee that you can cut an obtuse triangle into smaller triangles, all of which are acute? An obtuse triangle is a triangle with one obtuse angle. An acute triangle is a triangle with three acute angles. A right angle is neither acute nor obtuse.
If you can find such a dissection, what is the smallest number of acute triangles into which any obtuse triangle can be dissected?



