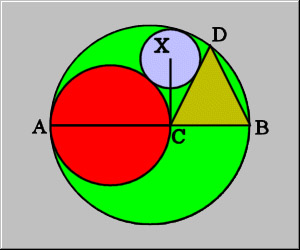
Consider a circle O with a diameter AB, shown here in green. Draw a second circle (red) with diameter AC, such that C is on AB. Draw an isosceles triangle with base CB and third vertex D on circle O. Draw a third circle (X), tangent to the first three figures. Prove that the line from C to the center of circle X is perpendicular to AB.
Thoroughly enjoyed this problem. Here's my solution:
Let w1 denote the red circle and w2 the green circle. Let r be the radius w1 and let R be the radius w2. Let x=2r(R-r)/(R+r). Draw a circle w3 externally tangent to w1 and internally tangent to w2 with radius x. Note that such a circle exists since x<R-r.
Let P, Q, and S be the centers of w1, w2, and w3, respectively. Let a=angle(PQS). Applying the law of cosines to triangle PQS, we have
PS^2 = PQ^2 + QS^2 - 2(PQ)(QS)cos(PQS)
or
(r+x)^2 = (R-r)^2 + (R-x)^2 - 2(R-r)(R-x)cos(a)
or, after some algebraic manipulation,
cos(a)=(R^2-Rr-Rx-rx)/((R-r)(R-x)).
Now note that
QC/QS = (2r-R)/(R-x),
which after some algebraic manipulation (making use of the fact that x=2r(R-r)/(R+r)), equals
-(R^2-Rr-Rx-rx)/((R-r)(R-x)),
or cos(180-a)=cos(180-PQS)=cos(CQS). This implies that triangle CQS is a right triangle with right angle at C. In other words, CS is perpendicular to AB. It would suffice to show that w3=X.
Now draw a line through C tangent to w3, "away" from w1. Let this line meet w2 at T and w3 at U. Drop a perpendicular from T to a point M on AB. Since CS and TM are parallel, we have that angle(SCT)=angle(CTM). Thus the right triangles CUS and TMC are similar, implying that
CU/US = TM/MC (Equation 1)
We can compute CU from the Pythagorean theorem on triangle CUS:
CU = sqrt(CS^2-SU^2). (Equation 2)
To get the value CS^2, we again need the Pythagorean theorem on triangle PCS:
CS^2 = PS^2 - CP^2
= (r+x)^2 - r^2
= x^2 + 2rx,
so plugging back into Equation 2,
CU = sqrt(x^2+2rx - x^2)
= sqrt(2rx).
Finally, plugging back into Equation 1,
sqrt(2rx)/x = TM/MC,
or letting MC = y,
TM = y*sqrt(2r/x).
Since TM is the altitude from the hypotenuse of right triangle ATB, we have the relation
TM^2 = AM*MB,
or
2ry^2/x = (2R-y-2r)(y+2r).
We can solve this equation for y. When we do so (using the relation x=2r(R-r)/(R+r)), we find:
y = R-r.
What does this mean? It means that M is the midpoint of CB, since we now have
BM = BA - AM
= BA - AC - CM
= 2R - 2r - y
= R-r
= y
= MC.
Thus, T coincides with the point D as described in the problem. It follows that w3 coincides with X, which completes the proof.





