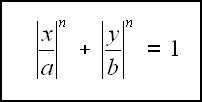There is a family of curves on the Cartesian plane described by this form:
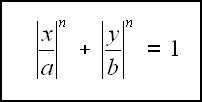
If n is equal to 2, then it describes an ellipse (if a = b, then it describes a circle).
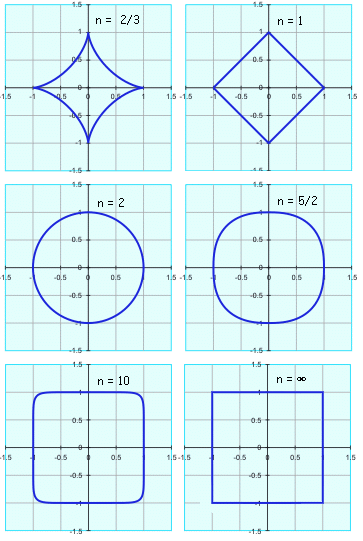
If n is greater than 2, then this is a "superellipse" (if a = b, then this is a supercircle).
As n increases, the ellipse becomes more "rectangularish", and as n approaches ∞, the limit is a rectangle (or a square if a=b).
What value must n have such that the figure has an area exactly halfway between the associated ellipse (when n=2) and rectangle (when n=∞)?
The graphs below, calculated by varying n with a = b = 1, show this property. Note that as n approaches zero, the curve degenerates into two crossed lines along the x- and y-axes.
(In reply to
Some thoughts by Federico Kereki)
Using Federico's formula, the numerical answer comes out to 3.16203795523.... The is based on the following program that iterates to the solution:
DECLARE FUNCTION lxf# (x#)
DEFDBL A-Z
FOR i = 1# TO 2 STEP .1#
' PRINT i, EXP(lxf(i - 1)) gamma function
NEXT
CLS
pi = ATN(1) * 4
n = 2
a = 2 ^ (2 - 2 / n) * SQR(pi) * EXP(lxf(1 / n) - lxf(1 / n - .5))
b = 2 ^ (2) * SQR(pi) * EXP(lxf(0) - lxf(-.5))
goal = (a + b) / 2
PRINT a, b, goal
n = 2.5
pV = 2 ^ (2 - 2 / n) * SQR(pi) * EXP(lxf(1 / n) - lxf(1 / n - .5))
pN = n
n = 3.5
v = 2 ^ (2 - 2 / n) * SQR(pi) * EXP(lxf(1 / n) - lxf(1 / n - .5))
DO
v = 2 ^ (2 - 2 / n) * SQR(pi) * EXP(lxf(1 / n) - lxf(1 / n - .5))
newN = pN + ((goal - pV) / (v - pV)) * (n - pN)
pN = n
pV = v
n = newN
PRINT pN, pV
LOOP UNTIL n = pN
PRINT n, v
FUNCTION lxf (x)
twopi = 8 * ATN(1)
IF x < 171 THEN
xm = x + 200
lo = LOG(xm) * (xm + .5)
lo = lo + (-xm + 1 / (12 * xm) - 1 / (360 * xm * xm * xm) + 1 / (1260 * xm * xm * xm * xm * xm))
lo = lo + LOG(twopi) / 2
FOR n = xm TO x + .5 STEP -1
lo = lo - LOG(n)
NEXT
ELSE
lo = LOG(x) * (x + .5)
lo = lo + (-x + 1 / (12 * x) - 1 / (360 * x * x * x) + 1 / (1260 * x * x * x * x * x))
lo = lo + LOG(twopi) / 2
END IF
lxf = lo
END FUNCTION
where the lxf function finds the log of x factorial, generalized to non-integers, explaining the need to subtract 1 from the argument to get the Gamma function.
The output is:
3.141592653589404 4.000000000000496 3.57079632679495
3.5 3.635880811932743
3.244712112757432 3.588231515882331
3.151300605038975 3.568451533688098
3.162373954713816 3.570869395064935
3.162039315800507 3.570796622710812
3.162037955050757 3.570796326755953
3.162037955230056 3.570796326793923
3.162037955234904 3.570796326796132
3.16203795523231 3.570796326795966
3.162037955216396 3.570796326792985
3.162037955226886 3.570796326793802
3.162037955241623 3.570796326798925
3.162037955230188 3.570796326793988
3.162037955232415 3.570796326796018
3.162037955231243 3.570796326794931
3.162037955231264 3.570796326794941
3.162037955231283 3.57079632679495
3.162037955231282 3.57079632679495
3.162037955231282 3.57079632679495
with the first line showing the values for n=2, n=inf and the average between the two. The successive convergents toward the solution are shown.
Plouffe's Inverter did not come up with a simple meaning for 3.162037955....
|
|
Posted by Charlie
on 2004-10-28 19:44:43 |