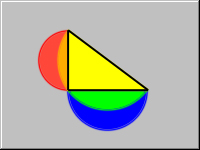
 Given a right triangle, draw the three following semicircles:
Given a right triangle, draw the three following semicircles:- The semicircle with diameter formed by one of the legs and extending away from the triangle.
- The semicircle with diameter formed by the other leg and extending away from the triangle.
- The semicircle with diameter formed by the hypotenuse and extending towards the triangle.
Prove that the area of the two crescents (shown in RED and BLUE) formed by the three semicircles equals the area of the triangle.



