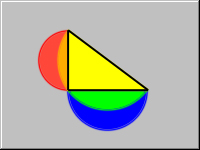
Given a right triangle, draw the three following semicircles:
- The semicircle with diameter formed by one of the legs and extending away from the triangle.
- The semicircle with diameter formed by the other leg and extending away from the triangle.
- The semicircle with diameter formed by the hypotenuse and extending towards the triangle.
Prove that the area of the two crescents (shown in RED and BLUE) formed by the three semicircles equals the area of the triangle.
In my post, Too Familiar, I thought it unfair to offer one of the many proofs I am familiar with. And then later I thought, like, no one here seems at all familiar with the Theorem of Thales, so, by gosh, I'm going to post it because it is, like, so neat. But I didn't want to post it if it was too redundant, so, while I was checking the Thales proof against those I know about, including Nikki's and Elisabeth's and Ray Kremer's winning proof for this same question which was posted at the Bradley University website in 1998, it occurred to me, hey, I have my own version of proof. I just hadn't realised it.
And, so, that's how it happened. Hugs. -CeeAnne-
|
|
Posted by CeeAnne
on 2004-10-13 05:49:14 |
About That Simpler Proof
