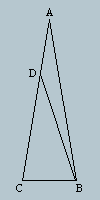
Triangle ABC has side AB=AC, and angle BAC = 20 degrees.
D is a point on side AC with AD=BC. Find angle DBC.
Solve this without trigonometry.
Iíve been trying to prove that angle DBC is 70 degrees without cheating, but Iíve only come "this close."
Before I get into the closest solution I have, I just wanted to throw out some ideas for others. In various attempts to use the AD = BC fact, here are some things that I didÖ they didnít get me anywhere, but maybe something will click for you that didnít click for me. Oh yeah, you donít have to do all of them. I put them into chunks, but I just decided not to restart the point naming process because that could get confusing.
Place a point E on line AB such that DE is parallel to BC. Next, place a point F on AB such that CF = BC. Since we know angle FBC is 80, and since we made triangle FBC isosceles, we know that angle FCB is 20, which shows that triangles FBC and DEA are at least similar. Since AD = BC, we know that they are actually congruent. This means that DE = BF. I donít know where that gets me, though. If I could prove that CF is perpendicular to DB, Iíd be home free. Then the triangle made by B, F, and the intersection of CF and DB would be a right triangle, and Iíd know the angle CFB = 80, so I could easily find angle ABD.
I also added a point G on line BC such that DG is parallel to AB, and a point H on line BC such that EH is parallel to AC. Calling the intersection of lines DG and EH point I, you can see that triangles ADE and IDE are congruent. Again, didnít get far with this.
And the last attempt I made was to perpendicularly bisect line DB. Call the midpoint of DB point J, and call the point where the perpendicular bisector intersects with AB point K. Due to SAS (DJ = JB, 90 = 90, JK = JK) we see that DK = KB, and triangles DJK and BJK are congruent. If I mirrored point K over line DB (and called the new point L), then triangles DKL and BKL are congruent, and both isosceles. Since I already found out (by cheating) that angle ABD is 10 degrees, I was hoping to find something that would prove that triangles DKL and BKL were at least similar to triangles ADE (or CBF). Then I would know that angle KBL was 20, and since I mirrored K over DB to get L, I know that angle ABD = Ĺ * angle KBL. But I didnít find out how to show that triangles DKL and BKL were similar to triangles ADE or CBF =(
Ok, now Iím going to go into the closest I got to proving anything from scratch. Now I will restart the letter naming, so if youíre trying to follow me you might want to start a new diagram. Note: I did not make this up on my own. I used the solution to Measure That Angle (I) and kind of worked backwards trying to solve this one.
First, I will say angle CAB = a, and angle ABC = b. Since triangle ABC is isosceles, this means that angle ACB = b as well. And since a = 20, we know that b = 80 (from a + 2b = 180). Iíll still keep using variables, though.
Place a point E along AB such that EB = BC. Next, bisect angle ABC, so both angles are b/2 (which we know is 40). The intersection of the bisector and AC will be called point F. So angle FBE = angle FBC = b/2.
Due to the SAS theorem, we see that triangles FBC and FBE are congruent (FB = FB, FBE = FBC, EB = BC). So the new information we get is FC = FE, angle FCB = angle FEC = b, and angle CFB = angle EFB. Angle CFB + angle CBF + angle FCB = 180 = angle CFB + b/2 + b, so angle CFB = 180 Ė 3/2*b (= 60). I will call this angle c.
Next, I want to do one of two things and somehow show that they are actually the same thing (but I donít know how to do that).
-
prove that triangle DEF = triangle BEF = triangle BCF. Then that will prove that DE = EB = BC = AD which should help me prove that angle ABD is 10, and thus angle DBC is 70. Since we know that EF = EF, and since we know numbers we know that angle DFE = angle BFE = angle BFC = angle c (=60), we are very close to having either SAS or ASA to prove the congruency. I wish I could just prove that angle DEF = angle BEF = b/2 = 40. Either that or FD = FB.
-
Create point G on line AC such that angle GEF = b/2. Then triangle GEF = triangle BEF = triangle BCF. Now Iíd just have to prove that G is coincident with D.
Hopefully Iíve given enough starts to the problem that someone else can bring it home.
|
|
Posted by nikki
on 2004-09-09 08:26:55 |
 Triangle ABC has side AB=AC, and angle BAC = 20 degrees.
Triangle ABC has side AB=AC, and angle BAC = 20 degrees.


