Below is an image of a square, 7 cm to a side, with four quarter-circles inscribed into it as showm.
Find the area of the shaded region in the center.
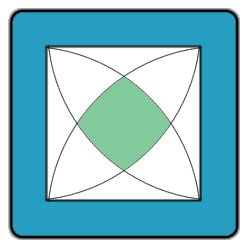
(In reply to
Any More? by Dulanjana)
The only trig I used was that sin(60 degrees) = √3/2. It's easy enough to get the same information without resorting to any trig notation - just show that the base of the large square and the top corner of the shaded area form an equilateral triangle. Drop a vertical line from the top corner to the base, and then use the Pythagorean theorm to show that the distance between the two is √3/2 x 7cm.
Incidentally, a slightly cleaner solution occurred to me, though it still uses many of the same elements as my last solution. Consider the pie wedge formed by the lower-right corner of the square and the top and right corners of the shaded area. Draw a point in the middle of the square, and draw lines between it and each of the three points in the wedge. Now you have three regions. One is exactly one quarter of the shaded area. The other two are triangles with easily calculated areas. Find the area of the wedge, then subtract out the areas of the triangles. Multiply that amount by 4, and you have the area of the shaded region.



