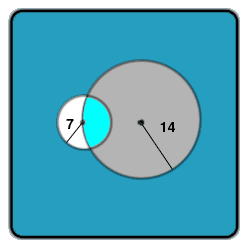
A circle has a radius of 14 cm. Another circle has a radius of 7 cm. The centre of the second circle lies on the circumference of the first. Find The common area for both circles.

(P.S -The answer might not be elegant)

Calculus solution using polar coordinates
Origin at center of small circle.
Small circle:   r=7
Large circle:   r=2Rcos(t)   where R is radius of big circle, t is angle from origin to a point on the circle (r,t)
               or,  r=28 cos(t)

Consider 2 segments.  For the first segment, imagine rotating a radius from origin, of length 7 from t=0 up to where the 2 circles intersect.  The second segment is from that angle up to pi/2.  Then double the segments.

The 2 circles intersect when r=7=28 cos(t).  ie cos(t)=1/4.  or when t=arccos(1/4).   Same as arcsin(sqrt(15)/4).

First segment (doubled):  2*integral from 0 to arccos(1/4) of (49/2) dt  which is= to    49 arccos(1/4)

Second segment (doubled):  is double integral of   r dr dt ;  the limits on the angle t are from arccos(1/4) up to pi/2.   The limits on r are from 0 up to the equation for the big circle.  so:
2* integral from arccos(1/4) to pi/2   integral from 0 to 28cos(t) of r dr dt.          The r dr, when integrated become r^2/2.   Since the upper limit of r is a function of t, we get a slightly more complicated function of t to integrate.           so:
2* integral from arccos(1/4) to pi/2  [cos^2(t)]/2  dt

integral of cosine squared of t is     .5*(t + sin(t)*cos(t))

Exact answer is:
49 arccos(1/4)  + 2*(14^2)[pi/2 - arccos(1/4)] - 2*(14^2)*sqrt(15)/16

= 68.7502555446012    the same as others found.