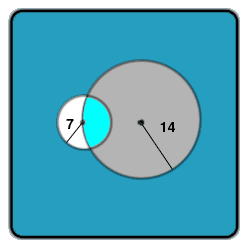
A circle has a radius of 14 cm. Another circle has a radius of 7 cm. The centre of the second circle lies on the circumference of the first. Find The common area for both circles.
(P.S -The answer might not be elegant)
The following calculus solution confirms those previously posted by lucky and then by myself, that had used trigonometry and area formulas. It also agrees with cris crawford's numeric answer, though the formula there didn't lead to that answer (perhaps a typo).
For ease of integration put the small circle centered at the topmost point on the larger one's circumference and place, while the larger one's center is at the origin. We need to integrate between the two curves y=√(14²-x²) and y = 14 - √(7²-x²), the latter being the lower part of the circle that's raised 14 units from the origin, from x=-√(735/16) to +√(735/16), the limits of integration being found from solving the equations simultaneously to find y=(2*14²-7²)/28, which leads to the above values of x.
Using Wolfram Research's on-line "The Integrator" on the difference between the above two functions, produces the indefinite integral
-14x+(x/2)√(49-x²)+(x/2)√(196-x²)+98arcsin(x/14)+(49/2)arcsin(x/7)
As this function is odd (f(-x)=-f(x)), in order to subtract the value at x=-√(735/16)from that at +√(735/16), we need only double the value at x=+√(735/16).
Using the UBASIC interpreter:
x=sqr(735/16)
OK
a=2*(-14*x+(x/2)*sqr(49-x^2)+(x/2)*sqr(196-x^2)+98*asin(x/14)+(49/2)*asin(x/7))
OK
?a
68.7502555446011987768
which, when rounded, is the answer posted previously by lucky, myself and cris crawford, using different methods.
|
|
Posted by Charlie
on 2003-02-15 14:46:55 |



