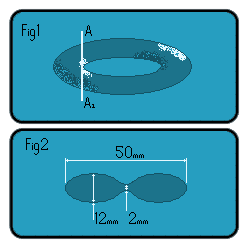
Take a regular torus (doughnut) shaped object and cut a vertical slice through it at line A-A1(Fig1).

Now look at the cross section formed(Fig2). Is it possible to calculate the volume of the original Torus? Prove your results.

Let's assume that the generating conic section for this torus is the usual circle, rather than an ellipse.  That is, when the torus is cut vertically through the center, the cross section would be two circles.

Then, as the height of the torus is 12 mm, the radius of the generating circle is 6 mm.  The cutting plane A-A1 leaves a band 2 mm wide, 1 mm either side of the horizontal center plane. How far is this cutting plane from the center of the generating circle? By the Pythagorean theorem, that's sqrt(6^2-1^2)=sqrt(35).

Then, looking down on the torus from above, we have a line that's the projection of A-A1 onto the center plane.  The thickness of the tube is 12 mm, so from the outer circle to the A-A1 plane is 6+sqrt(35). Use this as one leg of a right triangle.  The other leg is half the projection of A-A1, or 25 mm.  The hypotenuse, extending from one point on the outer circle to another, forming a chord, is then sqrt(25^2 + (6+sqrt(35))^2) = 27.6946377011362.  The angle at the base of this triangle is then arccos((6+sqrt(35))/sqrt(25^2 + (6+sqrt(35))^2)), but more importantly, that argument to the arccos is the sine of the angle at the center of the torus that subtends half that chord that had been the hypotenuse, and becomes the base of a right triangle with the radius of the outer circle as the new hypotenuse. The radius is then (sqrt(25^2 + (6+sqrt(35))^2) / 2) / ((6+sqrt(35))/sqrt(25^2 + (6+sqrt(35))^2)) = 32.1831076729198.  Then R, the radius of the torus used in computing the area, is 6 less than this, or 26.1831076729198. We've already determined r, the radius of the generating circle.

The volume formula is 2 * pi^2 * R * r^2. In this case, this works out to 18606.0178600448. For the record, that's ((sqr(25^2+(6+sqr(35))^2)/2)/((6+sqr(35))/sqr(25^2+(6+sqr(35))^2))-6)*pi^2*36*2.