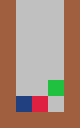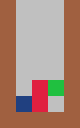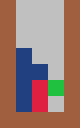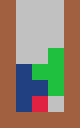A typical game of
Tetris has 10 columns and 7 pieces. Consider a variation with fewer columns and only one piece, which repeats indefinitely.
For some pieces and column widths it is trivial to see that an infinite game is possible. For example the I tetromino with any column width or any other of the
tetrominoes with an even column width.
For other pieces, an infinite game is possible, but not trivially so.
Consider the T tetromino in three columns, an infinite game is possible by following a pattern:
The first piece is horizontal with the stem of the T pointing down.
The second piece is vertical, with the stem of the T pointing to the right and the T is pushed to the left edge.
The third piece is vertical, with the stem of the T pointing to the left and the T is pushed to the right edge. |
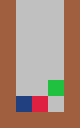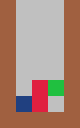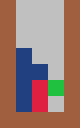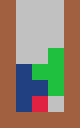
|
For each piece and number of columns listed below, find a strategy for each which allows for an infinite game:
1. 2.
### in three columns ### in four columns
# #
#
3. 4.
### in four columns ##### in five columns
# #
#
-----------------------------------------------------
Notes:
1 - Using the reflection of an asymmetrical piece is not allowed.
2 - Use classic gravity: when a row is filled, it is removed and all rows above move down, but no fragments of one partially filled row fall into another partially filled row.
1.
Let the first two drop without rotation, leaving a stack of 2 on the left, as the horizontal long arm of the piece completely disappears in each case:
|2 |
|1 |
+---+
Place the third one on the right in normal letter-L formation with the short arm on the bottom:
| 3 |
|23 | which becomes | 3 |
|133| |23 |
+---+ +---+
The next one will be an upside-down L on the right:
| 44|
| 34| | 44|
|234| which becomes | 34|
+---+ +---+
The fifth and sixth will come straight down:
|555|
|544| becomes then |666|
| 34| | 34| |634| disappears completely,
+---+ +---+ +---+
ready for a new start.
2.
The first piece goes to the bottom left with the stem pointing up:
| 1 |
| 1 |
|111 |
+----+
Then the second piece with stem pointing down, to the right of this:
| 222|
| 12 |
| 12 |
|111 |
+----+
The third piece:
|3 |
|333 | |3 |
|3222| |333 |
| 12 | becomes | 12 |
| 12 | | 12 |
|111 | |111 |
+----+ +----+
The fourth:
| 4| | |
|3444| | |
|3334| becomes | 4|
| 12 | | 12 |
| 12 | | 12 |
|111 | |111 |
+----+ +----+
The fifth:
| | | |
|5 | | |
|5554| |5 |
|512 | becomes |512 |
| 12 | | 12 |
|111 | |111 |
+----+ +----+
The sixth:
| | | |
| 6| | |
|5666| | |
|5126| | 6|
| 12 | becomes | 12 |
|111 | |111 |
+----+ +----+
The seventh:
| | | |
| | | |
|7 | | |
|7776| becomes |7 |
|712 | |712 |
|111 | |111 |
+----+ +----+
The eighth:
| | | |
| | | |
| 8| | |
|7888| | |
|7128| becomes | 8|
|111 | |111 |
+----+ +----+
There are only 8 members of this cycle as the next drop of an upward stem (upside down T) on the left:
| | | |
| | | |
| 9 | | |
| 9 | leaves | 9 |
|9998| | 9 |
|111 | |111 |
+----+ +----+
which actually replicates the result of the first drop, though the configuration is a combination of pieces from two pentominos. So play continues as in drop number 2.
3.
The first piece is placed:
| |
| |
| 1 |
| 1 |
| 111|
+----+
then pieces 2 and 3
| 333| | |
|2223| | 333|
| 123| leaves | 123|
| 12 | | 12 |
| 111| | 111|
+----+ +----+
and so forth:
|444 | | |
|4333| | |
|4123| leaves |444 |
| 12 | | 12 |
| 111| | 111|
+----+ +----+
| | | |
| 555| | |
|4445| leaves | 555|
| 125| | 125|
| 111| | 111|
+----+ +----+
| | | |
|666 | | |
|6555| leaves | |
|6125| |666 |
| 111| | 111|
+----+ +----+
two steps here, 7 and 8:
|7 | | |
|7888| | |
|7778| leaves | |
|6668| |7 |
| 111| | 111|
+----+ +----+
| | | |
| 9 | | |
| 9 | leaves | 9 |
|7999| | 9 |
| 111| | 111|
+----+ +----+
The last configuration is the same as after the first drop, so play continues as in drop number 2.
|
|
Posted by Charlie
on 2007-12-19 19:00:59 |