Three circles (A, B, and C) are tangentially connected:

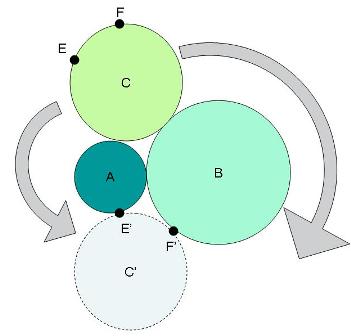
Properties:
1) Circle B's radius is twice the radius of Circle A.
2) Circle C is of the exact size that if it rolls around A, or it rolls around B, it will touch A and B on the opposite side at identical points E and F.

What is the radius of Circle C if:
1) C > B
2) B > C > A
3) A > C (C is a maximum)

First, treat this as if the rolling circle is starting in the C' position, and rolling completely around until it's in the C' position again. This allows the C position's rotation to be any arbitrary value, which it is.

If circle A has radius 1 and circle B radius 2 and C radius x, and the centers of the circles joined with line segments to make a triangle, then according to the law of cosines,

(2+x)^2 = 9 + (1+x)^2 - 6(1+x)cos A
cosA = (9 + (1+x)^2 - (2+x)^2)/(6(1+x))

and similarly

cosB = (9 + (2+x)^2 - (1+x)^2)/(6(2+x))

C = pi - A - B

Arc C is twice passed over from being tangent to either circle A or circle B. That means that the rolling portion of circle C has a total arc length of 2*pi*x - 2*C*x, where, again, C is the arc measure, in radians, of each of the two skipped over portions of circle C's circumference.

The actual contact length that is provided by A and B is

2*pi - 2*A + 2*(2*pi - 2*B)

These are to be equal for the congruence to work.  The following program solves this numerically:

DECLARE FUNCTION acos# (x#)
DEFDBL A-Z
PRINT
pi = ATN(1) * 4
stx = 2#: stp = .001#
DO
FOR x = stx TO 3 STEP stp
 a = ((9 + (1 + x) ^ 2 - (2 + x) ^ 2) / (6 * (1 + x)))
 b = ((9 + (2 + x) ^ 2 - (1 + x) ^ 2) / (6 * (2 + x)))
 IF ABS(a) <= 1 AND ABS(b) <= 1 THEN
   a = acos(a)
   b = acos(b)
   c = pi - a - b
   needed = 2 * pi * x - 2 * c * x
   achieved = 2 * pi - 2 * a + 2 * (2 * pi - 2 * b)
   diff = achieved - needed

   PRINT x, 2 * pi * x - 2 * c * x, 2 * pi - 2 * a + 2 * (2 * pi - 2 * b)
   IF diff < 0 THEN
     stx = x - stp: stp = stp / 10: PRINT stx; stp:
     OPEN "3circles.txt" FOR APPEND AS #2
     PRINT #2, stx; stp
     CLOSE
     EXIT FOR
   END IF
 END IF
NEXT
LOOP

FUNCTION acos (x)
 acos = ATN(SQR(1 - x * x) / x)
END FUNCTION

The successive approximations and the increment of x are given:

 2.527999999999942  .0001
 2.528299999999942  .00001
 2.528329999999943  .000001
 2.528337999999944  .0000001
 2.528338099999944  .00000001
 2.528338139999943  .000000001
 2.528338143999944  .0000000001
 2.528338143999944  .00000000001
 2.528338143999944  .000000000001
 2.528338144004944  .0000000000001
 2.528338144005244  .00000000000001
 2.528338144005295  .000000000000001
 2.528338144005302  .0000000000000001

indicating the radius of circle C is approximately 2.528338144005302.

This is requested case 1.

Other solutions require going around multiple times.

Posted by Charlie on 2007-12-27 20:15:37