My object was to create a unique 4 digit square number on each face. At the same time I required each vertex to be a 3 digit square. I failed in that objective!
I have 6 unique 4 digit squares but I have duplicated just one of my vertices.
To emulate my "feat":
- a [Magenta] Magenta cell is both the first digit of a 3 and 4 digit square
- an [Orange] Orange cell signifies the first digit of only a 4 digit square, while
- a [Cyan] Cyan cell signifies the first cell only of a 3 digit square.
The digits must be applied to each face by rotation, the direction is defined by need. "A" through "F" represent the 6 faces of the cube while "a" through "h" represent the vertices of the cube when fully assembled.
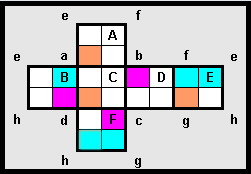
But then, there is still the challenge for 6 unique faces and 8 unique vertices.



