(In reply to
Computer solutions by Charlie)
The full output of 93 solutions (63 with one repeat vertex and 30 with no repeat vertices) follow:
15
16
63613269
91929412
65
74
1156 1369 9216 3249 1296 5476
361 361 529 169 441 729
169 1 361 2 441 1 529 1 625 1 729 1 961 1
15
16
63613269
91929412
65
74
1156 1369 9216 3249 1296 5476
361 361 529 196 441 729
196 1 361 2 441 1 529 1 625 1 729 1 961 1
15
16
49691268
23125211
62
11
1156 3249 1296 1225 1681 2116
961 169 225 361 121 121
121 2 169 1 225 1 361 1 625 1 841 1 961 1
15
16
49691268
23125211
62
11
1156 3249 1296 1225 1681 2116
961 196 225 361 121 121
121 2 196 1 225 1 361 1 625 1 841 1 961 1
52
12
24443116
64144847
41
67
1225 4624 1444 3481 4761 1764
441 324 144 441 784 676
121 1 144 1 324 1 441 2 625 1 676 1 784 1
52
12
24443116
64144847
41
67
1225 4624 1444 3481 4761 1764
441 324 144 441 784 676
121 1 144 1 324 1 441 2 625 1 676 1 784 1
52
12
24443116
64144847
41
67
1225 4624 1444 3481 4761 1764
441 324 144 441 784 676
121 1 144 1 324 1 441 2 625 1 676 1 784 1
52
12
24443116
64144847
41
67
1225 4624 1444 3481 4761 1764
441 324 144 441 784 676
121 1 144 1 324 1 441 2 625 1 676 1 784 1
52
11
61248952
56616442
73
21
1521 6561 6241 8649 4225 3721
121 841 361 676 144 225
121 1 144 1 225 1 256 1 361 1 529 1 676 1 841 1
52
11
61248952
56616442
73
21
1521 6561 6241 8649 4225 3721
121 841 361 676 144 225
121 1 144 1 225 1 256 1 361 1 529 1 676 1 841 1
52
11
24463116
64844847
41
67
1521 4624 8464 3481 4761 1764
441 361 144 484 784 676
121 1 144 1 361 1 441 1 484 1 625 1 676 1 784 1
52
11
24463116
64844847
41
67
1521 4624 8464 3481 4761 1764
441 361 144 484 784 676
121 1 144 1 361 1 441 1 484 1 625 1 676 1 784 1
52
11
24463116
64844847
41
67
1521 4624 8464 3481 4761 1764
441 361 144 484 784 676
121 1 144 1 361 1 441 1 484 1 625 1 676 1 784 1
52
11
24463116
64844847
41
67
1521 4624 8464 3481 4761 1764
441 361 144 484 784 676
121 1 144 1 361 1 441 1 484 1 625 1 676 1 784 1
12
15
64426529
71461616
43
63
1521 1764 4624 6561 1296 3364
441 625 361 144 361 676
144 1 225 1 361 2 441 1 625 1 676 1 961 1
12
15
64426529
71461616
43
63
1521 1764 4624 6561 1296 3364
441 625 361 144 361 676
144 1 225 1 361 2 441 1 625 1 676 1 961 1
61
21
76569635
75612146
71
64
2116 5776 6561 9216 4356 1764
625 961 121 576 441 676
121 1 361 1 441 1 576 2 625 1 676 1 961 1
61
29
53425632
64465259
12
16
2916 4356 4624 5625 5329 2116
324 529 256 441 625 169
169 1 256 2 324 1 361 1 441 1 529 1 625 1
61
29
53425692
64465259
12
16
2916 4356 4624 5625 5929 2116
324 529 256 441 625 169
169 1 256 2 324 1 441 1 529 1 625 1 961 1
61
29
53425692
64465259
12
16
2916 4356 4624 5625 5929 2116
324 529 256 441 625 169
169 1 256 2 324 1 441 1 529 1 625 1 961 1
61
29
53425632
64465259
12
16
2916 4356 4624 5625 5329 2116
324 529 256 441 625 196
196 1 256 2 324 1 361 1 441 1 529 1 625 1
61
29
53425692
64465259
12
16
2916 4356 4624 5625 5929 2116
324 529 256 441 625 196
196 1 256 2 324 1 441 1 529 1 625 1 961 1
61
29
53425692
64465259
12
16
2916 4356 4624 5625 5929 2116
324 529 256 441 625 196
196 1 256 2 324 1 441 1 529 1 625 1 961 1
22
45
51422116
61676165
95
23
4225 1156 6724 2116 6561 5329
144 225 576 169 361 256
121 1 144 1 169 1 225 1 256 1 361 1 576 1 625 1
22
45
51422116
61676165
95
29
4225 1156 6724 2116 6561 5929
144 225 576 169 961 256
121 1 144 1 169 1 225 1 256 1 576 1 625 1 961 1
22
45
51422116
61676165
95
29
4225 1156 6724 2116 6561 5929
144 225 576 169 961 256
121 1 144 1 169 1 225 1 256 1 576 1 625 1 961 1
22
45
51422116
61676165
95
23
4225 1156 6724 2116 6561 5329
144 225 576 196 361 256
121 1 144 1 196 1 225 1 256 1 361 1 576 1 625 1
22
45
51422116
61676165
95
29
4225 1156 6724 2116 6561 5929
144 225 576 196 961 256
121 1 144 1 196 1 225 1 256 1 576 1 625 1 961 1
22
45
51422116
61676165
95
29
4225 1156 6724 2116 6561 5929
144 225 576 196 961 256
121 1 144 1 196 1 225 1 256 1 576 1 625 1 961 1
22
45
51422116
61676165
95
23
4225 1156 6724 2116 6561 5329
144 225 576 169 361 256
121 1 144 1 169 1 225 1 256 1 361 1 576 1 625 1
22
45
51422116
61676165
95
29
4225 1156 6724 2116 6561 5929
144 225 576 169 961 256
121 1 144 1 169 1 225 1 256 1 576 1 625 1 961 1
22
45
51422116
61676165
95
29
4225 1156 6724 2116 6561 5929
144 225 576 169 961 256
121 1 144 1 169 1 225 1 256 1 576 1 625 1 961 1
22
45
51422116
61676165
95
23
4225 1156 6724 2116 6561 5329
144 225 576 196 361 256
121 1 144 1 196 1 225 1 256 1 361 1 576 1 625 1
22
45
51422116
61676165
95
29
4225 1156 6724 2116 6561 5929
144 225 576 196 961 256
121 1 144 1 196 1 225 1 256 1 576 1 625 1 961 1
22
45
51422116
61676165
95
29
4225 1156 6724 2116 6561 5929
144 225 576 196 961 256
121 1 144 1 196 1 225 1 256 1 576 1 625 1 961 1
52
42
63297952
91161256
29
16
4225 1369 1296 7921 5625 9216
324 729 961 121 625 169
121 1 169 1 256 1 324 1 529 1 625 1 729 1 961 1
52
42
63297952
91161256
29
16
4225 1369 1296 7921 5625 9216
324 729 961 121 625 196
121 1 196 1 256 1 324 1 529 1 625 1 729 1 961 1
52
42
63295952
43169211
61
81
4225 3364 1296 5929 1521 1681
324 529 169 361 121 841
121 1 169 1 256 1 324 1 361 1 529 2 841 1
52
42
63295952
43169211
61
81
4225 3364 1296 5929 1521 1681
324 529 196 361 121 841
121 1 196 1 256 1 324 1 361 1 529 2 841 1
52
42
63295952
43169211
61
81
4225 3364 1296 5929 1521 1681
324 529 169 361 121 841
121 1 169 1 256 1 324 1 361 1 529 2 841 1
52
42
63295952
43169211
61
81
4225 3364 1296 5929 1521 1681
324 529 196 361 121 841
121 1 196 1 256 1 324 1 361 1 529 2 841 1
98
44
81423922
28469675
11
25
4489 8281 4624 3969 7225 1521
144 324 169 841 576 225
144 1 169 1 225 1 289 2 324 1 576 1 841 1
98
44
81423922
28469675
11
25
4489 8281 4624 3969 7225 1521
144 324 196 841 576 225
144 1 196 1 225 1 289 2 324 1 576 1 841 1
98
44
81423922
28469675
11
25
4489 8281 4624 3969 7225 1521
144 324 169 841 576 225
144 1 169 1 225 1 289 2 324 1 576 1 841 1
98
44
81423922
28469675
11
25
4489 8281 4624 3969 7225 1521
144 324 196 841 576 225
144 1 196 1 225 1 289 2 324 1 576 1 841 1
98
44
81423922
28469675
11
25
4489 8281 4624 3969 7225 1521
144 324 169 841 576 225
144 1 169 1 225 1 289 2 324 1 576 1 841 1
98
44
81423922
28469675
11
25
4489 8281 4624 3969 7225 1521
144 324 196 841 576 225
144 1 196 1 225 1 289 2 324 1 576 1 841 1
98
44
81423922
28469675
11
25
4489 8281 4624 3969 7225 1521
144 324 169 841 576 225
144 1 169 1 225 1 289 2 324 1 576 1 841 1
98
44
81423922
28469675
11
25
4489 8281 4624 3969 7225 1521
144 324 196 841 576 225
144 1 196 1 225 1 289 2 324 1 576 1 841 1
98
44
88123442
96798446
62
11
4489 6889 7921 3844 4624 2116
841 324 289 676 144 169
144 1 169 1 289 2 324 1 484 1 676 1 841 1
98
44
88123442
96798446
62
11
4489 6889 7921 3844 4624 2116
841 324 289 676 144 169
144 1 169 1 289 2 324 1 484 1 676 1 841 1
98
44
88123442
96798446
62
11
4489 6889 7921 3844 4624 2116
841 324 289 676 144 196
144 1 196 1 289 2 324 1 484 1 676 1 841 1
98
44
88123442
96798446
62
11
4489 6889 7921 3844 4624 2116
841 324 289 676 144 196
144 1 196 1 289 2 324 1 484 1 676 1 841 1
48
51
86248474
11614674
98
46
5184 1681 6241 8464 7744 8649
625 841 841 169 676 441
169 1 441 1 484 1 625 1 676 1 784 1 841 2
48
51
86248474
11614674
98
46
5184 1681 6241 8464 7744 8649
625 841 841 169 676 441
169 1 441 1 484 1 625 1 676 1 784 1 841 2
48
51
86248474
11614674
98
46
5184 1681 6241 8464 7744 8649
625 841 841 196 676 441
196 1 441 1 484 1 625 1 676 1 784 1 841 2
48
51
86248474
11614674
98
46
5184 1681 6241 8464 7744 8649
625 841 841 196 676 441
196 1 441 1 484 1 625 1 676 1 784 1 841 2
67
54
92618661
61929421
67
93
5476 1296 9216 8649 2116 7396
256 841 729 169 324 961
169 2 196 1 256 1 324 1 676 1 729 1 841 1 961 1
67
54
92618661
61929421
67
93
5476 1296 9216 8649 2116 7396
256 841 729 196 324 961
169 1 196 2 256 1 324 1 676 1 729 1 841 1 961 1
67
54
56218662
11969444
61
81
5476 1156 9216 8649 4624 1681
625 841 196 169 144 841
144 1 169 1 196 1 256 1 625 1 676 1 841 2
67
54
56218662
11969444
61
81
5476 1156 9216 8649 4624 1681
625 841 196 169 144 841
144 1 169 1 196 1 256 1 625 1 676 1 841 2
67
54
56218662
11969444
61
81
5476 1156 9216 8649 4624 1681
625 841 169 196 144 841
144 1 169 1 196 1 256 1 625 1 676 1 841 2
67
54
56218662
11969444
61
81
5476 1156 9216 8649 4624 1681
625 841 169 196 144 841
144 1 169 1 196 1 256 1 625 1 676 1 841 2
67
54
16241663
92612988
51
22
5476 2916 6241 1296 8836 1225
625 144 121 256 289 289
121 1 144 1 256 1 289 2 361 1 625 1 676 1
67
54
16241663
92612988
51
22
5476 2916 6241 1296 8836 1225
625 144 121 256 289 289
121 1 144 1 256 1 289 2 361 1 625 1 676 1
56
61
69144752
93621672
11
56
6561 3969 6241 4761 7225 1156
961 441 121 361 676 529
121 1 256 1 361 1 441 1 529 1 576 1 676 1 961 1
56
61
69144752
93621672
11
56
6561 3969 6241 4761 7225 1156
961 441 121 361 676 529
121 1 256 1 361 1 441 1 529 1 576 1 676 1 961 1
16
65
22526761
51114292
24
25
6561 1225 1521 6724 9216 4225
256 625 441 121 529 225
121 2 225 1 256 1 441 1 529 1 625 1 676 1
72
64
63187976
43165614
62
19
6724 3364 1681 7569 1764 2916
361 784 256 361 961 144
144 1 256 1 361 2 676 1 729 1 784 1 961 1
72
64
63187976
43165614
62
19
6724 3364 1681 7569 1764 2916
361 784 256 361 961 144
144 1 256 1 361 2 676 1 729 1 784 1 961 1
72
64
69114115
57267616
95
23
6724 7569 2116 4761 1156 5329
961 441 576 729 361 256
121 1 256 1 361 1 441 1 576 2 729 1 961 1
98
68
65744921
16744896
61
92
6889 6561 7744 4489 9216 1296
576 484 144 676 289 961
144 1 169 1 196 1 289 2 484 1 576 1 676 1 961 1
98
68
65744921
16744896
61
92
6889 6561 7744 4489 9216 1296
576 484 144 676 289 961
144 1 169 1 196 1 289 2 484 1 576 1 676 1 961 1
52
72
25652972
11116164
23
49
7225 1521 1156 2916 6724 3249
576 225 361 121 961 441
121 1 225 2 361 1 441 1 576 1 729 1 961 1
52
72
26652976
44116141
43
48
7225 4624 1156 2916 4761 3844
676 225 361 441 841 441
225 1 361 1 441 2 625 1 676 1 729 1 841 1
52
72
26643976
44892441
45
81
7225 4624 8649 3249 4761 5184
676 324 529 484 144 841
144 1 324 1 484 1 529 1 625 1 676 1 729 1 841 1
52
72
26643976
44892441
45
81
7225 4624 8649 3249 4761 5184
676 324 529 484 144 841
144 1 324 1 484 1 529 1 625 1 676 1 729 1 841 1
56
79
25627522
21442245
43
63
7569 1225 4624 7225 4225 3364
576 729 324 144 324 625
144 1 225 1 256 1 324 2 576 1 625 1 729 1
56
79
25627522
21442245
43
63
7569 1225 4624 7225 4225 3364
576 729 324 144 324 625
144 1 225 1 256 1 324 2 576 1 625 1 729 1
56
79
25682916
24116165
43
63
7569 4225 1681 2916 6561 3364
576 289 361 441 361 625
169 1 196 1 289 1 361 2 441 1 576 1 625 2
92
71
25621567
24441254
88
36
7921 4225 4624 1521 5476 8836
576 121 841 484 625 324
121 1 324 1 484 1 576 1 625 2 729 1 841 1
92
71
25621567
27441254
88
36
7921 7225 4624 1521 5476 8836
576 121 841 784 625 324
121 1 324 1 576 1 625 2 729 1 784 1 841 1
92
71
26644565
44892211
45
81
7921 4624 8649 4225 1156 5184
676 441 529 484 121 841
121 1 441 1 484 1 529 2 625 1 676 1 841 1
46
84
22914193
57267616
95
23
8464 7225 2916 4761 1936 5329
289 441 576 729 361 256
256 1 289 1 324 1 361 1 441 1 576 1 729 1 961 1
46
84
22914193
57267616
95
29
8464 7225 2916 4761 1936 5929
289 441 576 729 961 256
256 1 289 1 324 1 441 1 576 1 729 1 961 2
46
84
22914193
57267616
95
29
8464 7225 2916 4761 1936 5929
289 441 576 729 961 256
256 1 289 1 324 1 441 1 576 1 729 1 961 2
46
84
12941768
69184611
67
93
8464 9216 1849 1764 1681 7396
289 144 784 961 361 961
144 1 289 1 361 1 676 1 784 1 841 1 961 2
46
84
12941768
69184611
67
93
8464 9216 1849 1764 1681 7396
289 144 784 961 361 961
144 1 289 1 361 1 676 1 784 1 841 1 961 2
46
84
22914193
57267616
95
23
8464 7225 2916 4761 1936 5329
289 441 576 729 361 256
256 1 289 1 324 1 361 1 441 1 576 1 729 1 961 1
46
84
22914193
57267616
95
29
8464 7225 2916 4761 1936 5929
289 441 576 729 961 256
256 1 289 1 324 1 441 1 576 1 729 1 961 2
46
84
22914193
57267616
95
29
8464 7225 2916 4761 1936 5929
289 441 576 729 961 256
256 1 289 1 324 1 441 1 576 1 729 1 961 2
46
84
12941768
69184611
67
93
8464 9216 1849 1764 1681 7396
289 144 784 961 361 961
144 1 289 1 361 1 676 1 784 1 841 1 961 2
46
84
12941768
69184611
67
93
8464 9216 1849 1764 1681 7396
289 144 784 961 361 961
144 1 289 1 361 1 676 1 784 1 841 1 961 2
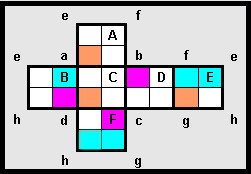
A couple of words of explanation of the prints are in order:
The Faces are listed in order, A through F.
The vertices are listed in order, except that e and f are not listed and must be derived from the diagram of the cube, as they were what was left, and merely verified they were squares.
The counts are accurate, except in some instances where the count is higher as in
67
54
92618661
61929421
67
93
5476 1296 9216 8649 2116 7396
256 841 729 196 324 961
169 1 196 2 256 1 324 1 676 1 729 1 841 1 961 1
where 196 is counted twice erroneously as vertex f is to be taken as 169 and not 196, and it is vertex d that is correctly counted as 196. Be assured there are 8 distinct squares accounted for at separate vertices.
|
|
Posted by Charlie
on 2008-05-02 17:23:07 |