|
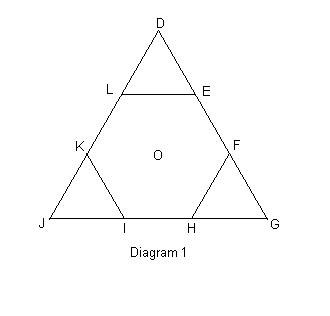
Let DGJ be an equilateral triangle. Mark the points E and F dividing the length DG into three equal segments. Mark the analogous points HI along GJ and KL along JD. Connect
FH, KI and EL to construct the regular hexagon DFHIKL (henceforth called M) and the three small equilateral triangles DEL, FGH, and IJK. (Henceforth called TD, TG and TJ). O, the centroid of DGJ, is simultaneously the centroid of M.
Case UVW:
Since U, V and W each lie closer to a vertex than to O, it follows that each point lies somewhere within one of the three small triangles: TD, TG or TJ. From examination of diagram 1,
it is immediately apparent that O will lie in UVW iff the three points are distributed, one each, in these small triangles. Since these smaller triangles have equal area, the probability of O occuring within UVW is 2/9, i.e., it is the probability that three items distributed randomly amongst three containers gives one item in each container.
�
Case XYZ:
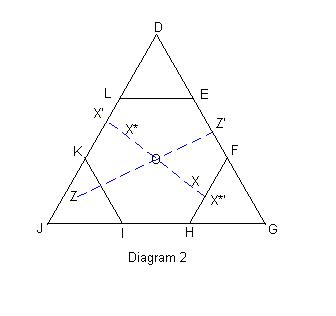
Since X,Y are closer to O than to any of the vertices, X,Y lie within the hexagon M. Draw the segments XO and ZO, extending them past O until they intersect hexagon M at the points X� and Z�, respectively. Then we can see that the triangle XYZ will contain O iff Y lies (within M) inside the sector X�OZ�.
Define X* = -X as the point on OX� such that OX* = OX. Now repeat the procedure of the preceeding paragraph to construct the sector X*�OZ', marking the locus of points Y such that X*YZ
contains O. Since XYZ and X*YZ have no area in common, O can appear in at most one of these triangles (see diagram 2). Further, since the angles X�OZ� and X*�OZ� sum to 180 degrees, the probability of O occuring within one of the two triangles is equal to the area of sector X*�FZ�ELX�X*� divided by the area of M. That is: one half. Finally, since X* is uniquely and reflexively determined from X, it follows that the probability of O occuring within XYZ is 1/4. |





