Place the numbers 1 to 9 once in each row, column, long diagonal (marked with a heavy dot) and every 3x3 grid.

The 'cage' inclusions (individually coloured regions) indicate the sum or the product of the numbers in those cells.

Unlike Killer Sudoku, the same number may appear more than once in a cage. So, 36x in a cage which overlaps the 3x3 grids may contain two 6s and a 1.


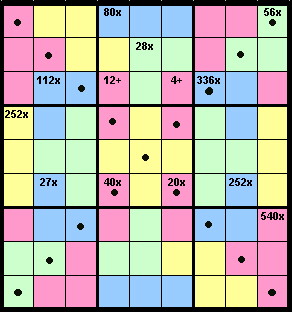My inspiration for this puzzle came from a variety of puzzles posted by Pete and Will at http://sudexel.com/forum/index.php

My thanks goes to brianjn for his hard work in producing the graphic.

(In reply to re(3): Solution by brianjn)

I created a spreadsheet of the "xy" 9 x 18 suggested previously.

With 2 cells making up one, each cell presented with a numeral and operator was supplied with a formula that drew on "lower half cells" of each referenced cage.

For comparison I copied the image that is in the body text and pasted it into my spreadsheet.

Outside the 9 x 18 grid I wrote formulae to sum each column, every second horizontal row of "half cells" and each diagonal.  [The sum in each case is 45].

With the image as a comparison, and the summations suggested, one would have a valid solution.

Having played for awhile I entered Penny's solution.

Yes, Dej Mar, I expect that from your description your approach was closely related; a worthy tool to assist a solution to problems such as this.

Edited on May 30, 2008, 4:56 am

Posted by brianjn on 2008-05-30 03:28:50