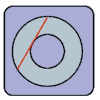
Remember
this problem? The one where you had to find the area between two circles by only knowing the length of the tangent "chord" (the red line)?
That problem is solved using some (moderately) tricky geometry. But if you know that the problem is solvable, it's actually pretty easy to solve by simply using the formula for the area of the circle and a bit of logic.
Can you do it?
Assume,
the radius of the larger circle = R
the length of the chord = 2L
Let L = q * R where 0<q<1 (as the chord length can vary between zero and the diameter)
By Pythagora's theorem, Radius of smaller circle r = ¡î(R©÷ - q©÷R©÷)
Area of the ring = Pi * R©÷ - Pi * r©÷
= Pi * R©÷ - Pi *(R©÷ - q©÷R©÷)
= Pi * q©÷R©÷
= Pi * (qR)©÷
= Pi * L©÷
Thus it can be seen that the solution is independent of the radius of the Circle, it only depends on the length of the chord.
Note - L is half-length of the chord.
|
|
Posted by Shiv
on 2004-10-12 05:10:24 |
 Remember this problem? The one where you had to find the area between two circles by only knowing the length of the tangent "chord" (the red line)?
Remember this problem? The one where you had to find the area between two circles by only knowing the length of the tangent "chord" (the red line)?



