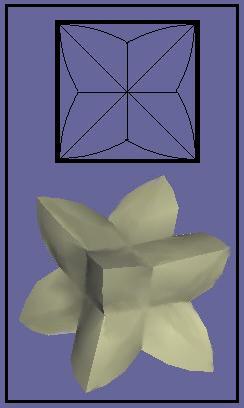
After four or five failed attempts at calculating the surfaced area using double integrals and surface formulas, I found a successful method, using single variable calculus. I thought about adding this as a problem in the queue (definitely D5), but I am probably the only person who would solve it anyways.
The surface of the object consists of 48 congruent segments. With the cube at lattice points (0,0,0)-(1,1,1), one segment can be defined by the cylinder y^2+(1-z)^2=1 and the planes y=1/2, x=1/2, x=z, and x=y.
A(,B,C) A B C
+------------*----+ +----*-----------_+
| * | | * / |
| * | | * _/ |
| * | y | * / |
| * | | * _/ |
| _P | a | * / |
| __/ *| x |* _/ |
| _/ *| i |* / |
| __/ *| s |* _/ |
| _/ * * / |
| __/ * * _/ |
|/ T(angle) * */ |
R-----------------* *-----------------+
D(,E,F) D E F
z axis x axis
(Sorry about the crude graphics)
Point A is at (0, 1/2, 1-sqrt[3]/2)
Point B is at (1-sqrt[3]/2, 1/2, 1-sqrt[3]/2)
Point C is at (1/2, 1/2, 1-sqrt[3]/2)
Point D is at (0, 0, 0) [The origin]
Point E is at (1-sqrt[3]/2, 0, 0)
Point F is at (1/2, 0, 0)
Point R is the cylinder's axis, (x,0,1)
Point P is a generic point on the cyninder (x,y,z).
ACDF is a segment of the cylinder and BCD is the segment whose area is in question.
BD is the intersection of plane x=z and the cylinder y^2+(1-z)^2=1. You can also verify it is the intersection of the cylinders y^2+(1-z)^2=1 and y^2+(1-x)^2=1.
CD is the intersection of the cylinder y^2+(1-z)^2=1 and plane x=y.
In a yz cross section the length of an arc, such as arc PD, equals the measure of angle PRD in radians. Then arc PD = angle T = arcsin(y) or arccos(1-z) or arctan(y/(1-z)). An integrable function can be formed by expressing y or z as a function of x.
Expressing curve BD in terms of x: (x, sqrt[2x-x^2], x)
Curve CD: (x, x, 1-sqrt[1-x^2])
The area of BDC equals area(BDE) + area(BCEF) - area (CDF)
The arc function for BCEF is a constant pi/6 radians, which makes the area of BCEF equal
pi(sqrt[3]-1)/12
I will express the other arc functions in terms of arcsin(y).
The arc function for CDF is arcsin(x) over the range [0, 1/2], which makes integral:
Integ{0,1/2}[arcsin(x)]dx
The substitution x=sin t changes the integral to
Integ{0,pi/6}[t*cos(t)]dt
Then using integration by parts u=t and dv=cos(t) dt, the integral can be evaluated as
pi/12 + sqrt(3)/2 - 1
The arc function for BDE is arcsin(sqrt[2x-x^2]) over the range [0, 1-sqrt[3]/2], which makes integral:
Integ{0, 1-sqrt[3]/2}[arcsin(sqrt[2x-x^2])]dx
The substitution sin t = sqrt[2x-x^2] successfully simplifies the integral to:
Integ{0,pi/6}[t*sin(t)]dt
Then using integration by parts u=t and dv=sin(t) dt, the integral can be evaluated as
1/2 - pi*sqrt[3]/12
Now the area of the segment can be expressed as
(1/2 - pi*sqrt[3]/12) + (pi(sqrt[3]-1)/12) - (pi/12 + sqrt(3)/2 - 1)
= 3/2 - pi/6 - sqrt[3]/2
Since there are 48 segments, the total surface area (assuming a 1x1x1 cube) is
72 - 8*pi - 24*sqrt[3]
That surface area is 88.3 percent of the cube's surface area.