In general,
find an integer
I which can be classified as Prime,
Triangle, Square or Cube, comprised of unique digits and when the digits are
rearranged, one of those categories applies.
[eg: 19 (P) → 91 (T)]
Then
specifically apply that rule to fill the table with the lowest values possible per category (integer I) with its anagram being larger, in the lower cell per category.
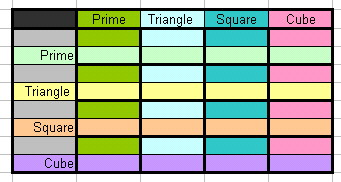Note: It may not be possible to offer solutions for all asymetric categories.
You might care also to offer some suggestions whereby some integers, without rearranging, may fall into another category -
36 (S), 36 (T); 729 (S), 729 (C).
Note that colours by row and column are category-defined.
DECLARE SUB permute (a$)
DECLARE FUNCTION anagram# (a$, b$)
DEFDBL A-Z
DIM num$(1000, 4)
PRINT
' Build table of primes, triangles, squares and cubes
num$(1, 1) = "2"
s = 2: i = 3
DO
good = 1
FOR j = 1 TO s - 1
IF i MOD VAL(num$(j, 1)) = 0 THEN good = 0: EXIT FOR
NEXT
IF good THEN
num$(s, 1) = LTRIM$(STR$(i))
s = s + 1
END IF
i = i + 1
LOOP UNTIL s > 1000
num$(1, 2) = "1"
s = 2: i = 2
DO
num$(s, 2) = LTRIM$(STR$(VAL(num$(s - 1, 2)) + i))
s = s + 1
i = i + 1
LOOP UNTIL s > 1000 OR LEN(num$(s - 1, 2)) > 4
num$(1, 3) = "1"
s = 2: i = 2
DO
num$(s, 3) = LTRIM$(STR$(i * i))
s = s + 1
i = i + 1
LOOP UNTIL s > 1000 OR LEN(num$(s - 1, 3)) > 4
num$(1, 4) = "1"
s = 2: i = 2
DO
num$(s, 4) = LTRIM$(STR$(i * i * i))
s = s + 1
i = i + 1
LOOP UNTIL s > 1000 OR LEN(num$(s - 1, 4)) > 4
' Match column against column to find results
FOR c1 = 1 TO 4
FOR c2 = 1 TO 4
FOR i = 1 TO 1000
found = 0
FOR j = 1 TO 1000
IF LEN(num$(j, c2)) > LEN(num$(i, c1)) THEN EXIT FOR
IF anagram(num$(j, c2), num$(i, c1)) THEN
found = 1
PRINT c1; c2, num$(i, c1); " "; num$(j, c2)
grid$(c1 * 2, c2) = num$(j, c2)
grid$(c1 * 2 - 1, c2) = num$(i, c1)
EXIT FOR
END IF
NEXT
IF found THEN EXIT FOR
NEXT
NEXT
NEXT
' Present grid of solutions
FOR c1 = 1 TO 4
FOR c2 = 1 TO 4
PRINT RIGHT$(" " + grid$(c1 * 2 - 1, c2), 5);
NEXT
PRINT
FOR c2 = 1 TO 4
PRINT RIGHT$(" " + grid$(c1 * 2, c2), 5);
NEXT
PRINT
PRINT
NEXT
' Expand to larger numbers to fill in triangle/cube gap
' triangle to cube
tr = 0
FOR i = 1 TO 3000
tr = tr + i
t$ = LTRIM$(STR$(tr))
IF LEN(t$) > 1 THEN
h$ = t$
DO
IF LEFT$(t$, 1) <> "0" THEN
v = VAL(t$)
cr = INT(v ^ (1 / 3) + .5)
IF cr * cr * cr = v THEN
PRINT tr; v, i; cr
EXIT FOR
END IF
END IF
permute t$
LOOP UNTIL h$ = t$
END IF
NEXT
' cube to triangle
FOR i = 1 TO 3000
cu = i * i * i
c$ = LTRIM$(STR$(cu))
IF LEN(c$) > 1 THEN
h$ = c$
DO
IF LEFT$(c$, 1) <> "0" THEN
v = VAL(c$)
tn = INT((SQR(1 + 8 * v) - 1) / 2 + .5)
IF tn * (tn + 1) = 2 * v THEN
PRINT cu; v, i; tn
EXIT FOR
END IF
END IF
permute c$
LOOP UNTIL h$ = c$
END IF
NEXT
END
FUNCTION anagram (a$, b$)
IF LEN(a$) <> LEN(b$) THEN anagram = 0: EXIT FUNCTION
IF a$ = b$ THEN anagram = 0: EXIT FUNCTION
x$ = a$
FOR i = 1 TO LEN(b$)
ix = INSTR(x$, MID$(b$, i, 1))
IF ix THEN
x$ = LEFT$(x$, ix - 1) + MID$(x$, ix + 1)
ELSE
anagram = 0: EXIT FUNCTION
END IF
NEXT
anagram = 1
END FUNCTION
The found anagrams (limited to 4-digit numbers or smaller):
From: \ to anagram:
prime tri sq cube
prime 13 19 61 251
anagram: 31 91 16 125
triangle 91 120 136
anagram: 19 210 361
square 16 361 144 1296
anagram: 61 136 441 9261
cube 125 2197 125
anagram: 251 7921 512
The triangle/cube spots are empty as they are 5-digit numbers:
226th triangular number = 25651; 15625 = 25^3
22^3 = 10648; 283rd triangular number = 40186
So to complete the table:
prime tri sq cube
prime 13 19 61 251
anagram: 31 91 16 125
triangle 91 120 136 25651
anagram: 19 210 361 15625
square 16 361 144 1296
anagram: 61 136 441 9261
cube 125 10648 2197 125
anagram: 251 40186 7921 512
When the anagrammed number must be larger than the original number, we get
prime tri sq cube
prime 13 19 163 251
anagram: 31 91 361 512
triangle 136 120 136 57970
anagram: 163 210 361 79507
square 16 1089 144 1296
anagram: 61 9180 441 9261
cube 125 10648 2197 125
anagram: 251 40186 7921 512
Note that the 25,651 to 15,625 triangle-to-cube anagram has disappeared completely. The other replacemed items are still present in the reverse direction.
The changed values come from programs like the following:
Prime to square:
5 N=10
10 while Found=0
20 N=nxtprm(N)
30 Ns=cutspc(str(N))
40 H=Ns:gosub *Permute(&Ns)
50 while H<>Ns
60 Sq=val(Ns)
70 Sr=sqrt(Sq)
80 if Sr*Sr=Sq then
90 :if Sq>N then
100 :print N,Sq
105 :Found=1
110 gosub *Permute(&Ns)
120 wend
130 wend
440 end
Square to triangular:
5 N=0
10 while Found=0
20 I=I+1:N=I*I
30 Ns=cutspc(str(N))
40 H=Ns:gosub *Permute(&Ns)
50 while H<>Ns
60 Sq=val(Ns)
70 Sr=int(sqrt(1+8*Sq)+0.5)
80 if Sr*Sr=1+8*Sq then
90 :if Sq>N then
100 :print N,Sq
105 :Found=1
110 gosub *Permute(&Ns)
120 wend
130 wend
440 end
Extra part:
The only prime that's a triangular number is 3.
No prime can be square or cube.
The squares that are cubes are all the 6th powers.
The following program:
DEFDBL A-Z
adr = 1
PRINT
DO
t = t + adr: adr = adr + 1
sr = INT(SQR(t) + .5)
IF sr * sr = t THEN PRINT t: ct = ct + 1
cr = INT(t ^ (1 / 3) + .5)
IF cr * cr * cr = t THEN PRINT SPACE$(20); t
LOOP UNTIL ct > 45
finds only 1 as being both triangular and cube. The following list shows those that are triangular and square:
1
36
1225
41616
1413721
48024900
1631432881
55420693056
1882672131025
the last triangular number checked when the program was interrupted being 22482404920990.
|
|
Posted by Charlie
on 2009-03-17 17:29:27 |
computer solution
