For the arbitrary triangle ABC in the figure below, prove that:
1) The yellow area is three times the cyan area.
2) The magenta area is five times the red area.
Note: The yellow and cyan areas are squares.
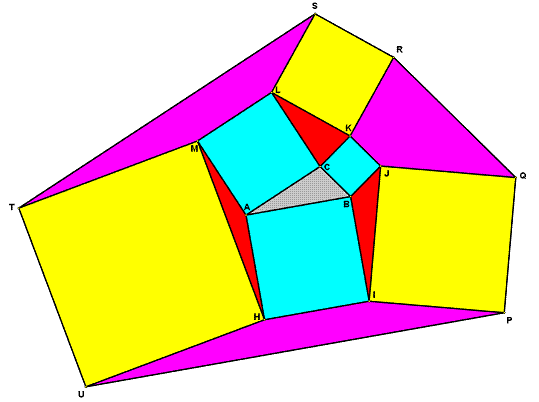
- Setup
Let the length of AB=c, AC=b, BC=a, IJ=y, KL=z, HM=x
Then BJ=JK=CK=BC=a, CL=LM=AM=AC=b, AH=HI=BI=AB=c, MT=TU=HU=HM=x, JQ=QP=IP=IJ=y, KR=RS=LS=KL=z
Also note supplementary angles: HAM = pi-BAC, IBJ = pi-ABC, and KCL = pi-ACB
- Find the lengths of x, y, z
Applying the law of cosines to triangles ABC, AHM, BIJ, and CKL yields:
a^2 = b^2 + c^2 - 2*b*c*cos(BAC)
b^2 = a^2 + c^2 - 2*a*c*cos(ABC)
c^2 = a^2 + b^2 - 2*a*b*cos(ACB)
x^2 = b^2 + c^2 - 2*b*c*cos(HAM)
y^2 = a^2 + c^2 - 2*a*c*cos(IBJ)
z^2 = a^2 + b^2 - 2*a*b*cos(KCL)
With the identity cos(A) = -cos(pi-A), x, y, and z can be expressed in terms of a, b, and c
x^2 = 2b^2 + 2c^2 - a^2
y^2 = 2a^2 + 2c^2 - b^2
z^2 = 2a^2 + 2b^2 - c^2
This is sufficient to prove part 1:
cyan area = a^2 + b^2 + c^2
yellow area = x^2 + y^2 + z^2 = 3*(a^2 + b^2 + c^2)
- Prove all four triangles ABC, AHM, BIJ, and CKL have the same area
Use the sine area formula on triangles ABC, AHM, BIJ, and CKL:
area(ABC) = (1/2)*b*c*sin(BAC)
area(ABC) = (1/2)*a*c*sin(ABC)
area(ABC) = (1/2)*a*b*sin(ACB)
area(AHM) = (1/2)*b*c*sin(HAM)
area(BIJ) = (1/2)*a*c*sin(IBJ)
area(CKL) = (1/2)*a*b*sin(KCL)
With the identity sin(A) = sin(pi-A), all four triangles ABC, AHM, BIJ, and CKL have the same area.
- Prove the three magenta quadrilaterals (MLST,JKRQ,HMTU) are trapezoids
Consider quadrilateral MLST
Let X be a point so that MX is an altitude of triangle MLT. MX is perpendictular to ML and TX.
Let Y be a point so that LY is an altitude of triangle MLS. LY is perpendictular to ML and SY.
Using the sine area formulas, triangles MLT and AHM have an equal area. (Similar to showing AHM and ABC have the same area)
Similarily triangles MLS and CKL have the same area.
AHM and CKL are known to have the same area as ABC, then MLT and MLS also have the same area as ABC. Since MLS and MLT have the same area and base ML, their altitudes MX and LY must be equal. Thst implies TX and SY are colinear which makes MLST a trapezoid with ML and ST parallel.
The other two magenta quadrilaterals JKRQ and HMTU are also trapezoids by the same logic.
- Find the area of MLST (and JKRQ and HMTU)
Let W be the area of ABC. Then W is also the area of AHM, CKL, MLT, and MLS. Since ML=b, the altitude of MLT and MLS equals 2*W/b by using area = 1/2 * base * altitude.
Z can also be expressed using Hero's formula: W = (1/4)*sqrt[2*a^2*b^2 + 2*a^2*c^2 + 2*b^2*c^2 - a^4 - b^4 - c^4]
MLST can be divided into three sections: MTX, MXYL, and LSY.
MXYL is a rectangle with dimensions b and 2*W/b, which makes an area of 2*W.
MTX is a right triangle with hypotenuse x and side 2*W/b, which makes an area of (1/2)*sqrt[x^2 - (2*W/b)^2]*(2*W/b)
Subsituting expressions for W and x and simplifying yields:
area MTX = (W/(2*b^2))*sqrt[9*b^4 - 6*a^2*b^2 + 6*b^2*c^2 - 2*a^2*c^2 + a^4 + c^4]
= (W/(2*b^2)) * (3b^2 - a^2 + c^2)
Triangle LSY is handled similarily to give an area of (W/(2*b^2)) * (3b^2 + a^2 - c^2)
The sum of areas MTX, MXYL, and LSY equals 5*W. Similarily JKRQ and HMTU also have an area of 5*W. The magenta trapezoids have a total area of 15*W and the red triangles have a total area of 3*W. This proves part 2.
One final note, using the trapezoid area formula can now tell us that ST=4*b, RQ=4*a, and PU=4*c



