Given a unit square and a fixed length, r.
Construct the set of all points which are at distance r from some point on the square.
Find the area of this set.
Note: A square is composed of 4 line segments, not the interior. For some values of r the set will have a hole in it.
Example of the construction:
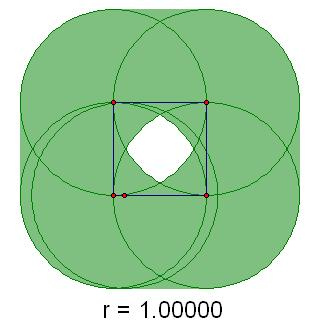
The area of the set is pi*r^2+4*r+1 minus the
area of the center hole.
For r < 1/2,
Area of center hole = (1-2*r)^2
For 1/2 <= r <= sqrt(2)/2,
No center hole
For sqrt(2)/2 < r,
Area of center hole
-- sqrt(r^2 - 1/4)
|
|
= 4 | [sqrt(r^2 - x^2) - 1/2] dx
|
|
-- 1/2
= 2*r^2*[arctan(t)-arctan(1/t)] - t + 1
where t = 2*sqrt(r^2 - 1/4) and
arctan returns radians.
|
|
Posted by Bractals
on 2009-10-01 14:41:27 |




