Given a unit square and a fixed length, r.
Construct the set of all points which are at distance r from some point on the square.
Find the area of this set.
Note: A square is composed of 4 line segments, not the interior. For some values of r the set will have a hole in it.
Example of the construction:
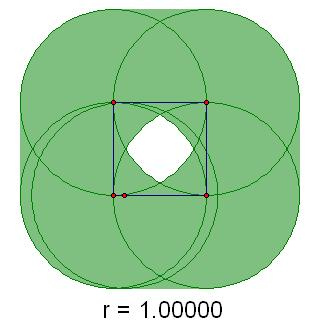
Bractals' and my formulas for the area of the center hole for r >= sqrt(2)/2 agree numerically:
DECLARE FUNCTION arcsin# (x#)
DEFDBL A-Z
FOR r = .8 TO 1.2 STEP .1
s = (SQR(1 + 4 * (r ^ 2 - 1 / 2)) - 1) / 2
theta = 2 * arcsin(s * SQR(2) / (2 * r))
a = (SQR(1 + 4 * (r ^ 2 - 1 / 2)) - 1) ^ 2 / 2 + 2 * r ^ 2 * (theta - SIN(theta))
PRINT USING "##.## ##.########"; r; a;
t = 2 * SQR(r ^ 2 - 1 / 4)
a = 2 * r ^ 2 * (ATN(t) - ATN(1 / t)) - t + 1
PRINT USING " ##.########"; a
NEXT
FUNCTION arcsin (x)
d = SQR(1 - x * x)
arcsin = ATN(x / d)
END FUNCTION
r Area(Charlie) Area(Bractals)
0.80 0.03328298 0.03328298
0.90 0.13956677 0.13956677
1.00 0.31514677 0.31514677
1.10 0.55792407 0.55792407
1.20 0.86664457 0.86664457
|
|
Posted by Charlie
on 2009-10-01 18:30:08 |




