Six chess knights are placed on a 4x3 chessboard, three along the top row and three along the bottom, which are labeled as P, Q, R, X, Y, Z, as shown in the figure below.
Exchange the positions of P and X, Q and Y and, R and Z, in minimum possible number of moves.
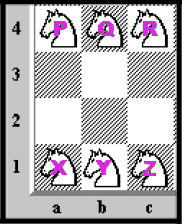
I think I may have found a solution in 62 steps, but I suspect I have retraced some steps. I have assumed that the knights can be moved in any order (i.e. they are neither "black" nor "white", so they need not alternate "sides"), but do note that PQR and XYZ must be in the same L to R sequences when they have exchanged ends of the board. I'll try my solution once more and see if it works. Perhaps others will have found a shorter sequence in any case.



