Six chess knights are placed on a 4x3 chessboard, three along the top row and three along the bottom, which are labeled as P, Q, R, X, Y, Z, as shown in the figure below.
Exchange the positions of P and X, Q and Y and, R and Z, in minimum possible number of moves.
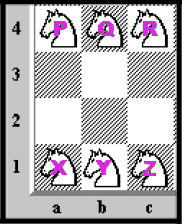
1. Take off all the pieces first.
2. Q to y is 3 moves*2 knights = 6
3. x to p is 5 moves*4 knights = 20
Therefore the minimum is 26.
Q and y can easily be made to translate without blocking (eg qa2, ya3; qb3, yc2; qb1, yb4.
So we can simply remove those squares from the board, if we can show that x can get from a1 to a4 without using them; e.g xc2,xa3,xc4,xb2,xc4 (not a unique solution) AND that this doesn't result in a roadblock during the translations requring a backward step:
xc2 xa3 x's next move is blocked, so
rb2 xc4 r's next move is blocked, so
pc3 ra4 xb2 pa2 rc3 xa4!
p's next move is blocked, so
zb3 za1 zc2 za3 zc4!
Then pc1 pb3 pa1!
Then ra2 rc1!
This requires 20 moves, so would seem to be a minimum solution, but no doubt there is a more analytical method.
|
|
Posted by broll
on 2010-04-06 05:13:45 |



