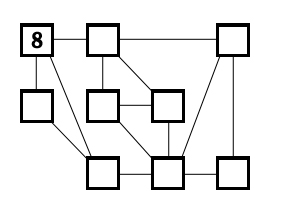
Place the numbers 1-9 in the boxes so that the difference of each pair of numbers joined by a line is at least three. The number 8 has already been placed.
(In reply to
Computer solution: not just for 8 by Charlie)
Ch,
Initially you claimed "The puzzle is solvable even when the 8 is replaced by 1, 2, 4 or 6."
Later you have added tHe digit 9, just providing 10 different solutions for the "extended" problem, rectifying a small error in your program.
Let me comment on the event.
In my opinion there is no better way of debugging a program than critically evaluate the final output , applying the basic "common sense" criteria.
In the case of the matrix abc,def,ghi, just by looking at the connectivity model it is clear that e and f are interchangeable having the same neighbors.
Also ,for any found solution, replacing all its digits follOwing a (k==>10-k) transformation we get a valid solution, i.e. there are 3 basic solutions:a1,a2,a4,and they generate a9,a8,a6.
Those 6 represent 12 solution ,if exchanging the values in e and f counts as a new configuration.
I discovered the lack of symmetry immediately when your initial result was published but since you corrected it I did not react.
Now I wrote about it just to emphasize the point I have mentioned above: ".. there is no better way of debugging a program than critically evaluate the final output".
No better remedy than common sense.
ADY
re: Computer solution: not just for 8
